|
University of Virginia Computer Science CS150: Computer Science, Fall 2005 |
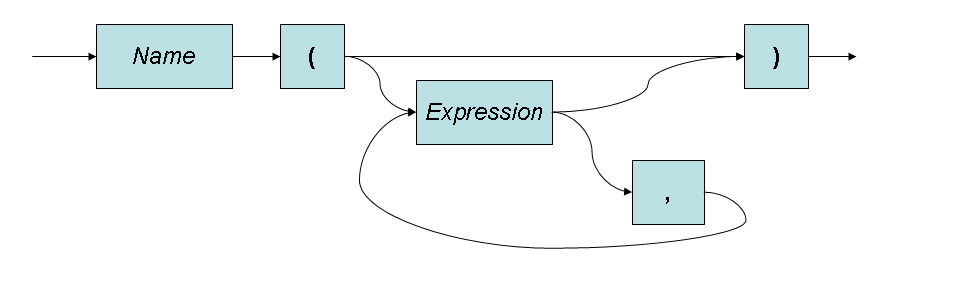
ApplicationStatement ::= Name ( Arguments )Draw a Recursive Transition Network that describes the same language as that generated by the ApplicationStatement above.
Arguments ::=
Arguments ::= MoreArguments
MoreArguments ::= Argument ,MoreArguments
MoreArguments ::= Argument
Argument ::= Expression

2. Santa Claus' procedure for identifying deserving children, as described in the famous lyric, is defined by:
(define (find-deserving children)
(filter is-nice? (filter is-nice? children)))
where the filter procedure was defined in listprocs.ss
(Problem Set 5):
(define (insertl f lst start)
(if (null? lst)
start
(f (car lst) (insertl f (cdr lst) start))))
(define (filter f lst)
(insertl
(lambda (el rest) (if (f el) (cons el rest) rest))
lst
null))
What is the complexity of Santa's find-deserving procedure?
Describe carefully the meaning of all variables you use in your answer
and any assumptions you make (for example, about the is-nice?
procedure used in find-deserving).
Comments: The find-deserving procedure is Θ(n) where n is the number of children (the length of the children parameter). This assume is-nice? is O(1) (that is, its time doesn't scale with the child).
The find-deserving procedure evaluates filter twice, first on the children list and then on the result of the first filter. We know the length of the list for the second filter evaluation is less than or equal to the length of the original list, since filter only removes elements. Hence, the complexity is dominated by the first filter evaluation. The filter procedure evaluates insertl on its input list. The insertl procedure cdrs down the input list, applying f to each element and the result for the rest of the list. As long as f is constant time, insertl is Θ(n) where n is the length of the input list (in this case, it matches the n used to represent the number of children).
3. Santa's elves make toys to distribute to the children. The global environment contains a variable toys that keeps track of all the available toys. It is a list of <toy, count> pairs, where the car of each pair is a string that uniquely identifies the toy and the cdr is the number of those toys available. For example, the list
(("smiley-puzzle" . 3253) ("aquadoodle" . 47382))
would mean that the elves have made 3253 smiley-puzzles and 47382 aquadoodles.
Define the procedure add-toy! that an elve calls after making a
toy.
It should take the name of a toy as its parameter and modify the global
toys list. If the toys list already contains an entry
whose
toy name matches the parameter name, then the count associated with that
toy should increase by 1. If there is no entry with the passed in toy
name, then a new pair should be added to the toys list that
contains the new toy name and count 1. Your add-toy! procedure
should
produce the following interactions:
Hint: you probably want to define an add-toy-helper! procedure that takes a list of toys as a parameter also, but be careful that your code mutates the global toys object.> toys
(("smiley-puzzle" . 3253) ("aquadoodle" . 47382))
> (add-toy! "smiley-puzzle")
> toys
(("smiley-puzzle" . 3254) ("aquadoodle" . 47382))
> (add-toy! "super-soaker"
> toys
(("smiley-puzzle" . 3254) ("aquadoodle" . 47382) ("super-soaker" . 1))
Comments: The hint was a bit misleading, since it makes more sense to have a non-mutating helper procedure that just finds the toy record.
(define (find-toy toys name)
(if (null? toys) null
(if (string=? (car (car toys)) name)
(car toys)
(find-toy (cdr toys) name))))
(define (add-toy! toy)
(let ((record (find-toy toys toy)))
(if (null? record)
(set! toys (append! toys (list (cons toy 1))))
(set-cdr! record (+ 1 (cdr record))))))
Note we need the set! in the true case, since toys
might be null originally.
Bonus. There are many elves working in parallel, each with their own Scheme interpreter, but there is one global toys list. Explain clearly what might go wrong it two elves apply your add-toy! procedure concurrently.
Comments: The procedure suffers from a race condition. If two elves make the same toy and evaluate add-toy! concurrently, it is possibly that the threads interleave in such a way that the number of toys only increases by one (for example elf 1 does (cdr record) to get the old count, elf 2 does (cdr record) to get the old count, elf 1 does the set-cdr! to increase the old count by one, and elf2 does the set-cdr! to increase the old count by one). If the toy is a new toy name, it is possible that there will be two records for the toy if both elves do find-toy before the first finished the append!.
4. After making the toys and identifying the nice children, Santa needs to match up the available toys with the nice children. He will go through the list of nice children and their wish lists, and then find the first requested toy that is available in the toys list. That it, the child's wist list is in order of most wanted to least wanted, and the child should receive the most wanted gift currently available on the toys list. (This approach is known as a greedy algorithm, see Class 35.)
Define the procedure match-toys! that matches a gift with each nice child. As input it takes a list of <child, wishlist> pairs where the wishlist is a list of toys wanted by the child ordered by preference. It should use the global toys object that initially reflects all the toys made by elves. Once a toy is matched with a child, it should be removed from the toys list. As output, it should produce a list of <child, toy> pairs where the toy is the avaliable toy that best matches the child's wishlist or null if there is no matching toy available.
For example, your match-toys! procedure should work like this:
> toys
(("smiley-puzzle" . 3254) ("aquadoodle" . 47382) ("super-soaker" . 1))
> (match-toys! (list (cons "Huey" (list "super-soaker" "smiley-puzzle")) (cons "Dewey" (list "super-soaker" "smiley-puzzle")) (cons "Louie" (list "super-soaker"))))
(("Huey" "super-soaker") ("Dewey" "smiley-puzzle") ("Louie" null))
> toys
(("smiley-puzzle" . 3253) ("aquadoodle" . 47382) ("super-soaker" . 0))
Comments:
(define (match-toy! wishlist)
(if (null? wishlist) null
(let ((record (find-toy toys (car wishlist))))
(if (null? record)
(match-toy! (cdr wishlist))
(if (> (cdr record) 0) ; some toys left
(begin
(set-cdr! record (- (cdr record) 1))
(car record))
(match-toy! (cdr wishlist)))))))
(define (match-toys! wishlists)
(map (lambda (wishlist)
(cons (car wishlist) (match-toy! (cdr wishlist))))
wishlists))
5. What is the complexity of your match-toys! procedure?
(Be sure to define any variables you use clearly and state all your
assumptions.)
Comments: There are three properties of the input size that we need variables to represent: c, the number of children; t, the number of toys; and w, the average length of a child's wishlist. We assume the string comparisons (string=? done in find-toy are constant time (this is probably a reasonable assumption since the length of the toy names are bounded).
The match-toys! procedure uses map to evaluate match-toy! for each child. This means the total work will be c times the amount of work for each match-toy! evaluation.
The match-toy! procedure takes a child's wishlist as its parameter. It cdr's down the wishlist, evaluating find-toy for each request until a matching toy is found. The find-toy procedure cdr's down the toys list until it finds the toy record. This requires up to t iterations, so it is Θ(t). If the child's wish is not found, we have to evaluate find-toy up to w times where w is the length of the wishlist.
Hence, the complexity is Θ(cwt).
6. Note that the greedy algorithm used by match-toys! does not produce an optimal mapping, since Louie did not get any toy even though there is a way of mapping toys to nice children where everyone child gets something on their list. Consider the optimal MatchToys problem described below:
Input: A list of <toy, count> pairs, and a list of <child, wishlist> pairs where the wishlist is list of toys requested by the associated child in preference order.Explain as clearly as possible how you would prove the MatchToys problem is NP-Complete.Output: A list of <child, toy> pairs where (1) each toy appears no more than its count number of times in the list, and (2) the list maximizes the toy utility function which is 3*number of children who got their first choice toy + 2 * number of children who got their second choice toy + 1 * number of children who got their third choice toy. (Note that children who list more than three toys on their wishlists are considered greedy and do not satisfy the "being nice" requirement, so they do not get a toy.)
Comments: To prove that a problem is NP-Complete we need to (1) show that it is in class NP, and (2) show that a known NP-Complete problem can be reduced to it. To show (1), we just need to argue that if you could try all possible solutions at once, it is easy to check if a solution is correct. We can do this, since there is a straightforward linear time procedure that checks the utility of a given match. To show (2), we need to show that we can transform an instance of a known NP-Complete problem into an instance of the MatchToys problem and use the result to solve the original problem. A good choice for the known NP-Complete problem is the 3SAT problem. To carry out the proof, we would need to find a mapping between a 3SAT instance and a MatchToys input. This is the tricky part, but our intuition should give us a good level of confidence that it would be possible.
7. Explain what the NP-Completeness of the MatchToys problem means for Santa.
Comments: It is intractable to solve NP-Complete problems for large input sizes, so unless Santa has a large qubit quantum computer or has solve P=NP by finding a polynomial time solution, we know Santa cannot solve the MatchToys problem as stated in any reasonable amount of time. Instead, he must settle for an approximation that is not guaranteed to find the best toy match. He could use a greedy algorithm like in Question 5. This would mean children should get their wishlists in early if they want to get the good presents before they run out.
8. In addition to matching toys with children, Santa must also deliver all the toys on time. Consider the CanDeliverOnTime problem:
Input: A list of <child, location, toy> triples where the location values are the longitude and latitude location of the child who should receive the toy; v, the maximum velocity of Santa's sleigh; and t, the amount of time available to deliver all the toys.Is the CanDeliverOnTime problem decidable or undecidable? Support your answer with a clear and convincing argument.Output: If there is an ordering of the list so that Santa can deliver all the toys to all the childern at the given locations, starting from the North Pole, and travelling at velocity v within time t, output true. Otherwise, output false. (Note that the laws of physics do not apply to Santa. His reindeer can travel at constant velocity v, and there is no problem with exceeding the speed of light, and it takes no time to drop off a toy once the correct location is reached.)
Comments: The CanDeliverOnTime problem is decidable. We can prove a problem is decidable by describing a procedure that is guaranteed to solve it in a finite amount of time. In this case, we can define a procedure that enumberates all possible orderings and checks them all. The number of orderings is finite (it is c! where c is the number of children) and the time required to check each ordering is also finite (Θ(c). The problem may be intractable (in fact, it is NP-Complete), but it is defrinitely decidable since we know it can be solved by a procedure that always eventually terminates.
9. In Class 30 we argued that HTML was not a universal language because there was no way to describe an infinite loop in HTML. Suppose the following construct was added to HTML to make HTMLR:
Element ::= <repeat> Elements </repeat>The meaning of <repeat> Elements </repeat> is to keep repeating Elements.
Is HTMLR a universal language? Support your answer with a clear and convincing argument.
Comments: No, HTMLR is not a universal language. Even with the repeat construct, it cannot do many computations that a Turin machine could do. For example, it has no way of making decisions (like if).
10. Appendix B of the Google paper argued (somewhat unconvincingly) that because the amount of human-generated content is finite, text indexing algorithms can be made near-linear, and processors are improving exponentially, that the fraction of content covered by web search engines will continue to improve. Assume in 2005 that Santa is able to finsh evaluating
(match-toys! (join-with-lists (find-deserving children) wish-lists)by December 24th to be able to deliver presents on time if the book on naughty or niceness is closed on December 1. (That is, it takes Santa 24 days to complete the evaluation.)
The join-with-lists procedure matches each deserving child with that child's wishlist. It is Θ(n log w) where n is the number of children (the length of the list passed as its first parameter) and w is the number of wishlists. (This assumes the wishlists are sorted and the children are not.)
Predict what Santa's naughty/nice cut-off date will be in 2011. Explain your answer at least as convincingly as Google's Appendix B.
Comments: We need to consider two things: how the input size of the problem changes and how the computing power available to Santa changes.
We consider the input size first. From question 5, we know match-toys! is Θ(cwt) where c is the number of children, w is the average wishlist length, and t is the total number of toys. Since join-with-lists scales slower, we do not need to consider its complexity. We assume children are not getting any greedier (this is probably false, but its hard to quantify how much greedier children are likely to get), so w does not change. The increase in c depends on the number of children serviced by Santa. According to the UN's Population predictions, the world population in 2010 is expected to be 6.8 Billion people, compare to 6.45 Billion people today. The question asked for 2011, so we will use 6.9 Billion as the population guess, and assume the number of children is a constant fraction of the population. We're making gross estimates here — the population increase is (/ 6.9 6.45) = 1.0697.
The number of toys, t should scale with the number of children unless Santa is willing to have deserving children unhappy on Christmas. So,em>t = k * c where k is constant, the work is increasing as Θ(c2). With the estimated children count increase, this means the work increase is (square 1.0697) = 1.1444.
Fortunately, Santa's computing power is also increasing according to Rudoplh's law (doubling every 18 months). There are 6 years until 2011, so that allows for 4 doublings or a fator of 16 improvement in computing power.
The time required in 2005 is 24 days. Scaling by the increase work would take (* 24 1.14444) days using today's computers. Dividing by 16 to reflect the improvements in computing power, gives 1.7166 days. This is good news for Santa, but bad news for children! Instead of only being good through December 1, children in 2011 will need to be good through December 22.
[Update, 24 December] Apparently, the business opportunity here has not elluded Google's all-encompassing eye. See Google's Blog.
|
CS 150: Computer Science University of Virginia |
evans@virginia.edu Using these Materials |