|
University of Virginia Computer Science CS150: Computer Science, Fall 2005 |
| Problem Set 4: Creating Colossi | Due: 26 September 2005 |
Collaboration Policy - Read Carefully
This problem set is intended to help you prepare for Exam 1. You may work on it by yourself or with other students, but you will need to do the exam on your own.
Regardless of whether you work alone or with a partner, you are encouraged to discuss this assignment with other students in the class and ask and provide help in useful ways. You may consult any outside resources you wish including books, papers, web sites and people. If you use resources other than the class materials, indicate what you used along with your answer.
| You have only one week to complete this problem set. We recommend you start early and take advantage of the staffed lab hours. |
Purpose
| Download: Download ps4.zip
to your machine and unzip it into your home directory
J:\cs150\ps4.
This file contains:
|
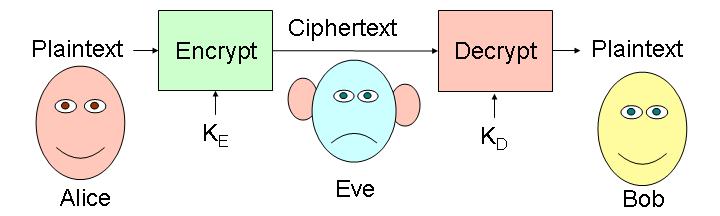
Since making up good encrypt and decrypt functions and keeping them secret is hard, most cryptosystems are designed to be secure even if the encryption and decryption algorithms are revealed. The security relies on a key which is kept secret and known only to the sender and receiver. The key alters the encryption and decryption algorithm in some way that would be hard for someone who doesn't know the key to figure out. If the sender and receiver use the same secret key we call it a symmetric cipher. If the sender and receiver can use different keys we call it an asymmetric cipher.

Ciphertext = ((encrypt KE) Plaintext))
Plaintext = ((encrypt KD) Ciphertext))
If KE = KD it is symmetric encryption
If KE is different from KD it is asymmetric encryption
(Cryptographers always talk about Alice and Bob, since Alyssa P. Hacker and Ben Bitdiddle have no secrets.)

Bletchley Park (Summer 2004) |
Question 1: For each f and g pair
below, argue convincingly whether or not f is
(1) O(g), (2) Ω(g), and (3)
Θ(g) as explained above. For all questions, assume n is a
non-negative integer.
|
In cryptography, it is usually easier to deal with 1 and 0 instead of true and false. For this problem set, use 1 to represent true and 0 to represent false. We will call each 0 or 1 a bit, since this is the smallest unit of information.
| Question 2: Define the xor function that takes two bits as parameters and evaluates to 1 if exactly one of the parameters is 1 and evaluates to 0 otherwise. |
Your xor function should produce these evaluations:
|
> (xor 0 0) 0 > (xor 0 1) 1 |
> (xor 1 0) 1 > (xor 1 1) 0 |
Fortunately for the allies, the Nazis didn't have a way of generating and distributing perfectly random bit sequences. Instead, they generated non-random sequences of bits using rotors. The Soviet Union also used a one-time pad cipher following WWII. Because their key bits were not truly random, and because they sometimes reused keys, the NSA was able to decrypt many important KGB messages. Details of this were released in 1995, and are available at the NSA's web site. We will look at how the Lorenz cipher used xor to encrypt messages soon. First, we consider how to turn messages into sequences of bits.
Table 1 shows the letter mappings for the Baudot code. For example, the letter H is represented by 10100 while I is 00110. We can put letters together just by concatenating their encodings. For example, the string "HI" is represented in Baudot as 10100 00110. There are some values in the Baudot code that are awkward to print: carriage return, line feed, letter shift, figure shift and error. For our purposes we will use printable characters unused in the Baudot code to represent those values so we can print encrypted messages as normal strings. Table 1 shows the replacement values in parenthesis.
| A | 00011 | H | 10100 | O | 11000 | V | 11110 | space | 00100 | ||||
| B | 11001 | I | 00110 | P | 10110 | W | 10011 | carriage return (,) | 01000 | ||||
| C | 01110 | J | 01011 | Q | 10111 | X | 11101 | line feed (-) | 00010 | ||||
| D | 01001 | K | 01111 | R | 01010 | Y | 10101 | letter shift (.) | 11111 | ||||
| E | 00001 | L | 10010 | S | 00101 | Z | 10001 | figure shift (!) | 11011 | ||||
| F | 01101 | M | 11100 | T | 10000 | error (*) | 00000 | ||||||
| G | 11010 | N | 01100 | U | 00111 |
We can use lists of ones and zeros to represent Baudot
codes. H is represented as (list 1 0 1 0 0). A
string is represented as a list of these lists: "HI" is
(list (list 1 0 1 0 0) (list 0 0 1 1 0)).
We have provided these two functions in lorenz.ss:
You can convert a string to a list of characters using string->list, and turn a list of characters into a string using list->string:
> (string->list "HI") (#\H #\I) > (list->string (list #\H #\I)) "HI"
| Question 3: a. Write a function string-to-baudot that takes a string and transforms it into a list of Baudot codes. b. Write the inverse function, baudot-to-string, that takes a list of lists of baudot codes and transforms it back into a string. c. Describe the complexity of your baudot-to-string procedure using Θ notation. Make sure to explain carefully what any variable you use means. |
Your functions should be inverses. Hence, you can test your code by
evaluating baudot-to-string composed with
string-to-baudot. For example,
(baudot-to-string (string-to-baudot "HELLO"))
should evaluate to "HELLO".
 Lorenz Cipher Machine |
The first 5 wheels were called the K wheels. Each bit of the Baudot representation of a letter was xor-ed with the value showing on the respective wheel. The same process was repeated with the next 5 wheels, named the S wheels. The resulting value represented the encrypted letter. After each message letter the K wheels turn one rotation. The movement of the S wheels was determined by the positions of the final two wheels, called the M wheels.
Like most ciphers, the Lorenz machine also required a key. The key was the starting position of each of the 12 wheels. To decipher the message you simply need to start the wheels with the same position as was used to encrypt and enter the ciphertext. There were 16,033,955,073,056,318,658 possible starting positions. This made the Nazis very confident that without knowing the key (starting positions of the wheels), no one would be able to break messages encrypted using the Lorenz machine. (But, their confidence was misplaced.)
Since the full Lorenz cipher would be too hard for this problem set, we will implement a simplified version. You should be suitably amazed that the allied cryptographers in 1943 were able to build a computer to solve a problem that is still hard for us to solve today! (Of course, they did have more that a week to solve it, and more serious motivation than we can provide in this course.)
Our Lorenz machine will use 11 wheels, each with only 5 positions. The first five wheels will be the K wheels and the second five the S wheels. Each of these will only have a single starting position for all 5 — that is, unlike the real Lorenz machine, for this problem set we will assume all five K wheels start in the same position and all five S wheels start in the same position.
The final wheel will act as the M wheel. After each letter all the K wheels and the M wheel should rotate. If the M wheel shows a 1 the S wheels should also rotate, but if the M wheel shows a 0 the S wheels do not rotate.
We have provided 3 lists that represent the wheels. The first is called K-wheels and is a list of lists, each of the inner lists containing the 5 settings. The definition is: (define K-wheels (list (list 1 1 0 1 0) (list 0 1 0 0 1) (list 1 0 0 1 0) (list 1 1 1 0 1) (list 1 0 0 0 1))).
There is a similar list called S-wheels to represent the S wheels of our simulated machine. The final list represents the M wheels and is just a single list. The definition is (define M-wheel (list 0 0 1 0 1)).
| Question 4: To rotate our wheels, we will take
the number at the front of the list and move it to the back. The first
number in the list will represent the current position of the wheel.
a. Define a function rotate-wheel that takes one of the wheels as a parameter. It should return the wheel rotated once. For example, (rotate-wheel (list 1 0 0 1 0)) should evaluate to (0 0 1 0 1). Although all the wheels in our simulated Lorenz cipher machine have five bits, your rotate-wheel procedure should work for any length list.
b. Define a function rotate-wheel-by that takes a wheel as the first parameter and a number as the second. The function should return the wheel list rotated by the number passed in. For example, (rotate-wheel-by (list 1 0 0 1 0) 2) should evaluate to (0 1 0 1 0) and (rotate-wheel-by wheel 5) should evaluate to wheel. |
| Question 5: a. Define a function rotate-wheel-list that takes a list of wheels (like K-wheels) as a parameter and evaluates to a list of wheels where each of the wheels in the parameter list of wheels has rotated once. For example, (rotate-wheel-list K-wheels) should evaluate to ((1 0 1 0 1) (1 0 0 1 0) (0 0 1 0 1) (1 1 0 1 1) (0 0 0 1 1)). b. Define a function rotate-wheel-list-by that takes a list of wheels and a number as parameters, and evaluates to a list where each of the wheels in the parameter list of wheels has rotated the number parameter times. For example, (rotate-wheel-list-by K-wheels 5) should evaluate to the same list as K-wheels. c. Describe the complexity of your rotate-wheel-list-by procedure using Θ notation. Be sure to explain what all variables you use mean. |
Now that we can rotate our wheels, let's figure out how to implement Lorenz encryption using our K and S wheels. Since both sets of wheels are doing the same thing, we should be able to write one procedure that will work with either the K wheels or the S wheels.
| Question 6: Define a function wheel-encrypt that takes a Baudot-encoded letter (a list of 5 bits) and a list of wheels as parameters. The function should xor each bit of the Baudot list with the first value of its respective wheel and return the resulting list. For example, (wheel-encrypt (list 0 0 0 1 1) K-wheels) should produce (1 0 1 0 0). Your wheel-encrypt procedure should be Θ(n) where n is the length of the list passed as the first parameter to wheel-encrypt. Argue convincingly why your wheel-encrypt procedure is Θ(n). |
We now have all the procedures we need to implement our simplified Lorenz machine. A quick review of how the machine should work:
| Question 7: a. Define a function called do-lorenz that takes a list of Baudot values, the K wheels, S wheels and M wheel. The function should encrypt the first Baudot code with the K and S wheels, then recursively encrypt the rest of the Baudot codes with the wheels rotated. The function should return the encrypted values in the form of a list of Baudot values. b. Define a function lorenz that takes four parameters: a string and three integers. The integers represent the starting positions of the three wheels, respectively. The function should call do-lorenz with the string converted to Baudot and the wheels rotated to the correct starting positions. The function should return the ciphertext in the form of a string. |
You should now be able to encrypt strings using the simplified Lorenz cipher. To test it, call your lorenz function with a string and offsets of your choice to produce ciphertext. Since our encryption and decryption functions are the same, if you evaluate lorenz again using the ciphertext and the same offsets you should get your original message back.
The messages were sent to John Tiltman at Bletchley Park. Tiltman was able to discern both messages and determine the generated key. The messages were then passed on to Bill Tutte who, after two months of work, figured out the complete structure of the Lorenz machine only from knowing the key it generated. The British were then able to break the Lorenz codes, but much of the work needed to be done by hand, which took a number of weeks to complete. By the time the messages were decrypted they were mostly useless.
The problem was given to Tommy Flowers, an electronics engineer from the Royal Post Office. Flowers designed and built a device called Colossus that worked primarily with electronic valves. The Colossus was the first electronic programmable computer. It was able to decrypt the Lorenz messages in a matter of hours, a huge improvement from the previous methods. The British built ten more Colossi and were able to decrypt an enormous amount of messages sent between Hitler and his high commanders. The British kept Colossus secret until the 1970s. After the war, eight of the Colossi were quickly destroyed and the remaining two were destroyed in 1960 and all drawings were burnt. The details of the breaking of the Lorenz Cipher were kept secret until 2000, but are now available at http://www.codesandciphers.org.uk/documents/newman/newmix.htm.
 Colossus (Original, 1943) |
 Colossus (Rebuilt, 2004) |
Our simplified cipher will be much easier to break. Since there are only 5 starting positions for the K wheels, 5 for the S wheels, and 5 for the M wheel, there are only 125 different keys. This is such a small number that we can simply try every possibility and look at the results to find the original message. Breaking a cipher by trying all possible key values is called a brute-force attack.
| Question 8: Define a procedure that takes a ciphertext and evaluates lorenz on the ciphertext for all 125 possible starting positions. It may be helpful to use the function printf that will print out a string to the interactions window. |
To test your procedure, try decrypting the following ciphertext (defined as
ciphertext in ps4.ss, don't try and type it in yourself!):
(define ciphertext
"GR-!-EN .H.CVZQZMRRFKSF QV*L!LO-TP
IY,PG.VUPNWKSNBVRUEW COXORUVJJNVD-SL*ZYCZVSU. MQTNLU PBEJ-FJVSF
CXRUER KZOEGUUBLWKUVBW,MYEWM.RLST,OZIKKW*ZUUUUVSWWXQXH,IITOMQG
VUUXA*JSGWSACW.")
If your procedure works correctly, one of the messages generated will look like sensible English.
| Question 9:
a. The actual Lorenz cipher operated similarly to the one in this problem set except instead of only having 5 positions in each wheel, each wheel had many more positions (up to 61). Suppose n is the number of possible positions for each Lorenz cipher wheel, and the procedure used to cryptanalyze the cipher is the same as your code (except extended as necessary to handle the extra wheel positions). Describe how the amount of work needed to break a Lorenz-encrypted message grows as a function of the number of wheel positions, n, using Θ notation. Assume the message length and number of wheels are fixed. b. Suppose instead that it was possible to add S and K wheels to the Lorenz cipher, and w represents the number of S and K wheels (for example, for the cipher machine in the problem set, w is 5). Describe how the amount of work needed to break a Lorenz-encrypted message grows as a function of w, using Θ notation. Assume the message length and number of wheel positions are fixed. c. If the Nazis learned of Bletchley Park's success in breaking the Lorenz cipher during the war, what changes that could be done without building and redistributing completly new cipher machines, would be most likely to prevent further successful cryptanalysis? |
Avail yourself of these means to communicate to us at seasonable intervals
a copy of your journal, notes & observations of every kind,
putting into cipher whatever might do injury if betrayed.Thomas Jefferson's instructions to Captain Lewis for the Expedition to the Pacific.
The complete text is available from
http://www.th-jefferson.org/html/instructions.html.It is regretted that it is not possible to give an adequate idea of the fascination of a Colossus at work: its sheer bulk and apparent complexity; the fantastic speed of thin paper tape round the glittering pulleys; the childish pleasure of not-not, span, print main heading and other gadgets; the wizardry of purely mechanical decoding letter by letter (one novice thought she was being hoaxed); the uncanny action of the typewriter in printing the correct scores without and beyond human aid; the stepping of display; periods of eager expectation culminating in the sudden appearance of the longed-for score; the strange rhythms characterizing every type of run; the stately break-in, the erratic short run, the regularity of wheel-breaking, the stolid rectangle interrupted by the wild leaps of the carriage-return, the frantic chatter of a motor run, the ludicrous frenzy of hosts of bogus scores.
D. Mitchie, J. Good, G. Timms. General Report on Tunny, 1945. (Released to the Public Record Office in 2000). http://www.alanturing.net/tunny_report
| Credits: This problem set was created for CS200 Spring 2002 by Jon Erdman and David Evans, and tested by Stephen Liang. It was revised for CS200 Spring 2003 and CS150 Fall 2005 by David Evans. |
|
CS 150: Computer Science University of Virginia |
evans@virginia.edu Using these Materials |