cs1120: Notes 9
Assignments Due
- Wednesday, 23 September: Problem Set 3
- Friday, 25 September: Read through Chapter 6
find-closest
(define (find-closest-number goal p)
(if (null? (cdr p))
(car p)
(if (< (abs (- goal (car p)))
(abs (- goal (find-closest-number goal (cdr p)))))
(car p)
(find-closest-number goal (cdr p)))))
Avoiding Duplicate Work
(define (pick-closest goal a b)
(if (< (abs (- goal a)) (abs (- goal b))) a b))
(define (find-closest-number goal p)
(if (null? (cdr p))
(car p)
(pick-closest goal
(car p)
(find-closest-number goal (cdr p)))))
Generalizing
(define (pick-minimizer f a b)
(if (< (f a) (f b)) a b))
(define (find-minimizer f p)
(if (null? (cdr p))
(car p)
(pick-minimizer f (car p)
(find-minimizer f (cdr p)))))
Use find-minimizer to define a procedure that finds the largest
number in a list of positive integers:
Music and Recursion
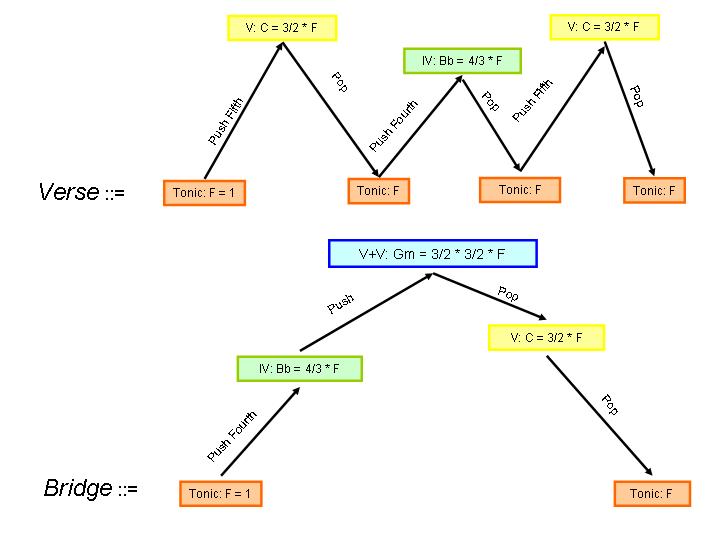
Song ::= Verse VBBD VBBD Better Coda
VBBD ::= Verse Bridge Bridge Dadada (ends on C)
Coda ::= F Eb Bb F Coda
Note: the Coda has no base case, and should continue forever (time permitting).
Challenge Problems
Define a Scheme procedure that can produce the INT and Gplot graphs from GEB Chapter 5. Hint: you may need to think about curves differently from PS3. (A solution is worth two gold stars.)
Find a "pop" song that has a recursive stack at least three deep.
Hofstadter's Law: It always takes longer than you expect, even when you
take Hofstadter's Law into account.