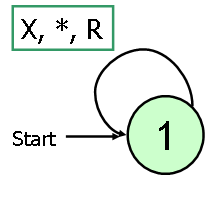
The simplest TM that never repeats a configuration requires only one state. It just keeps wiring new symbols on the tape:
| Final - Comments |
For each of the following questions you are asked to write a procedure that solves the described problem. You may write your procedure using any programming language you want (although we expect it will be easiest to answer these questions well using Scheme). If you use a language other than Scheme, PHP, SQL, Ada, Algol, BASIC, C, C++, C#, CLU, FL, Fortran, Haskell, Java, ML, Pascal, Python or Smalltalk for your answer, include a URL to a reference manual for the language you use in your answer.
1. (Average 9.8/10; 18/21 = 10, 21/21 >= 8) Combine Lists
Input: Two equal length lists of numbers.For example, (combine-lists (list 1 2 3) (list 4 5 6)) should evaluate to ((1 . 4) (2 . 5) (3 . 6)).
Output: A list containing elements that are pairs of the corresponding elements in the input lists.
Answer: The simplest procedure is:2. (Average 7.95; 6 = 10, 13 >= 8) Count Matches(define (combine-lists a b) (map cons a b))Without using map, we can define combine-lists as:(define (combine-lists a b) (if (or (null? a) (null? b)) null (cons (cons (car a) (car b)) (combine-lists (cdr a) (cdr b)))))
Input: Two (possibly non-equal length) lists of numbers, a comparison functionFor example:
Output: A count of the number of elements for which the comparison function applied to the corresponding elements in the two input lists evaluates to true. If the is no corresponding element (one list is shorter), the element should not be counted.
> (count-matches (list 1 2 3) (list 2 4 6) =) 0 > (count-matches (list 1 2 3) (list 0 2 4 6 8 10) =) 1 > (count-matches (list 1 2 3 4) (list 0 1 4) >) 2
Answer: There are many different strategies for defining count-matches. One approach is to use combine-lists defined in question 1:3. (Average 9.25; 15 = 10, 18 >= 8) Disjunct(define (count-matches a b f) (length (filter (lambda (pair) (f (car pair) (cdr pair))) (combine-lists a b))))We could also define it recursively as:(define (count-matches a b f) (if (or (null? a) (null? b)) 0 (+ (if (f (car a) (car b)) 1 0) (count-matches (cdr a) (cdr b) f))))
Input: Two procedures, p and qFor example, ((disjunct > =) 3 4) should evaluate to false and ((disjunct < =) 3 3) should evaluate to true.
Output: A procedure that takes two parameters and evaluates to true only if applying p to both parameters evaluates to true or applying q to both parameters evaluates to true.
Answer:
(define (disjunct p q)
(lambda (a b) (or (p a b) (q a b))))
(define (map2d f ll)
(map (lambda (inner-list) (map f inner-list)) ll))
Express your answer using Θ notation. Be sure to justify it with
an explanation and to fully describe what any variables you use in your
answer mean, and any assumptions you need to make.
Answer: The input to map2d is a list of lists. We measure the input size n as the total number of elements in all the inner lists, and use m as the number of elements in the outer list. The procedure uses map on the outer list first, this is Θ(m). For each element in the outer list, it evaluates, (map f inner-list). Hence, f is evaluated n total times, once for each element in the inner lists. Thus, the total work is Θ(m + n * work(f)). If we assume f is Θ(1) (that is, the time f takes does not depend on the input), we have, Θ(m + n). Now, if we assume the inner lists are not empty, we know n >= m, and can simplify this to Θ(n).5, 6 and 7. (Average 23.1/30; 9 answers correctly identified PEP as undecidable; no answers identified Chess Problem as easiest) (Counts as 3 questions) How would a theoretician order the problems below from least difficult to most difficult? Justify your answer by explaining how much work each problem involves using Θ notation (or explaining why the problem is undecidable). Be careful to fully describe what any variables you use in your answer mean, and any assumptions you need to make.Another acceptable answer was to assume the inner lists are of average length n (which must be >= 1), and that the number of elements in the outer list is m. Then, the total work is Θ(mn).
Ali G ProblemInput: Two long d-digit numbers (mostly nines)Chess Problem
Output: The product of the two input numbersInput: A chess position (a list of pieces on a 64 square board)Genome Assembly ProblemOutput: If there is winning strategy for white (moves first), output true (that is, a way of moving for white that guarantees a win no matter what the adversary does). Otherwise, output false.
Input: A set of genome reads (sequences of base pairs)Procedure Equivalence ProblemOutput: The smallest possible genome that includes each read.
Input: Two procedures, P and Q, each taking one input that can be any value. You may assume both procedures are guaranteed to always terminate.Output: true is P is functionally equivalent to Q; false otherwise. Two procedures are functionally equivalent if for every input the produce the same output.
Answer: The theoretitican will order the problems according to their theoretical complexity, without considering how large typical inputs are or how adequate good approximations are.Hardest: Procedure Equivalence Problem
The general Procedure Equivalence Problem is undecidable. If we could solve it, we could define halts? as:(define (halts? P) (not (procedure-equivalence P infinite-loop)))With the stated assumption that both procedures are guaranteed to always terminate, it is less obvious, but it is still undecidable. The two procedures are equivalent only if they produce the same result for all possible values, and the input may be any value. There are infinitely many inputs, so there is no way to execute the procedures on all of the inputs. The only way to prove equivalence is to examine the code, but it is undecidable to determine equivalence this way. If we could, we could solve other known undecidable problems, such as the "prints 3" problem from Lecture 26.Second Hardest: Genome Assembly Problem
This problem is NP-Complete (see Lecture 39).Third Hardest: Ali G ProblemThis problem is O(d2) (see Lecture 35).Easiest: Chess ProblemNearly everyone put this hardest or second hardest (and no one correctly rated it as easiest), but it is (theoretically) actually the easiest! The reason it is so easy is because there are only a finite number of possible inputs. In theory, we could know the answer for all possible chess positions, and implement the Chess Problem as a simple lookup table. Hence, it is O(1), and the easiest of the four problems. The fact that we don't actually know what the lookup table is, and it would need to be huge are not of concern to the theorist: it is finite. Note that the input size for this problem is also fixed: the maximum size input is chess position on a 64 square board. Answers which used n but didn't define what n means don't make sense, since there is no clear way to measure the size of the input to this problem.8-9. (Average: 14.95/20) (counts as 2 questions) How would a pragmatist order the same problems? If the amount of work is different for the pragmatist, explain clearly why. You should assume your pragmatist cares about getting a reasonably good answer to the problem today. State any assumptions you make about what the actual input size is, and how good and answer is "good enough".Answer: Unlike the theoretical ordering which is fairly clear (that is, it would be hard to argue that some other ordering from the one in the answers is "correct"), there are many "correct" orderings for the pragmatist which could be justified.One approach would be to consider how well each of the problems has been solved already:
Hardest: Chess Problem or Procedural Equivalence Problem
We have programs that can play chess very well, but none that can come close to solving the Chess Problem. Note that a solution to the Chess Problem would be able to take the standard starting chess position and say, "Its a win for white" (meaning that there is a way for white to move that guarantees a win, no matter what black does). This would effectively end chess as a game.Third Hardest: Genome Assembly ProblemThe Procedural Equivalence Problem is theoretically undecidable (and hence, impossible to solve in general), but we can approximate it or solve it for some subset of procedures reasonably well. When I graded your answers to questions 1-3, I was solving the Procedural Equivalence Problem, deciding if your procedure was equivalent to a correct procedure. This could have been automated by testing your procedure on a set of carefully selected inputs, and comparing them to the outputs from the correct procedure on those inputs. This would not guarantee they are the same, since there are infinitely many possible inputs, but would give a good indication. For more complex programs, it is very difficult to determine equivalence. This is one of the things my research group works on.
A good approximation of the human genome was announce in June 2000 (see Lecture 39), so we know this problem can be solved practically. Doing so required billions of dollars and several years of effort using some of the world's most powerful computers.Easiest: Ali G ProblemThe computers in ITC labs do a pretty good job solving this one, even for ridiculously large numbers. If you use DrScheme, you get an exact value. With Excel, you get a pretty good approximation.
Answer: I was surprised how many people claimed this was impossible. Reading the exam comments would have been a good idea, especially as there is a direct link to the relevant question here!11. The goal of this course is to teach students to think like computer scientists, and the goal of this exam is to measure how well you have done that so I can fairly determine your final grade. If you feel your answers on this exam will not adequately demonstrate what you have learned, or that I should take other things into account in determining your final grade, use this space to explain why.The simplest TM that never repeats a configuration requires only one state. It just keeps wiring new symbols on the tape:

A few people commented that they thought the exam weighted complexity too heavily, which I think is probably true (although, I do believe your answers to the complexity questions gave me pretty good insight into whether or not you were thinking about problems in the right way). I calculated the exam grades with two different weightings — one counted all the problems equally, one counted questions 5-9 as 1.5 questions total. If the second weighting improved your score, that is the score I used (marked as "W: score" on your exam).The overall average without the weighting adjustment was 81.25; with the weighting adjustment 84.07.