| Problem Set 3: L-System Fractals |
Out: 4 February 2002 Due: 13 February 2002, before class |
Turn-in Checklist:
On February 13, bring to class a stapled turn in containing:
|
Collaboration Policy - Same as Problem Set 2
For this problem set, you may either work alone and turn in a problem set with just your name on it, or work with one other student in the class of your choice. If you work with a partner, you and your partner should turn in one assignment with both of your names on it.PurposeRegardless of whether you work alone or with a partner, you are encouraged to discuss this assignment with other students in the class and ask and provide help in useful ways. You may consult any outside resources you wish including books, papers, web sites and people. If you use resources other than the class materials, indicate what you used along with your answer.
- Learn to use lists
- Write recursive functions that manipulate lists
- Introduce data abstraction
- Make some better fractals than you could in PS2
Downloads
- curve.ss — updated from Problem Set 2
- lsystem.ss — partial code for L-System Fractals
Background
In Problem Set 2, you created fractals by manipulating functions that represented curves. In this problem set, you will explore a different way of creating fractals known as the Lindenmayer system (or L-system). Aristid Lindemayer, a theoretical biologist at the University of Utrecht, developed the L-system in 1968 as a mathematical theory of plant development. In the late 1980s, he collaborated with Przemyslaw Prusinkiewicz, a computer scientist at the University of Regina, to explore computational properties of the L-system and developed many of the ideas on which this problem set is based.
The idea behind L-system fractals is we can describe a curve as a list of lines and turns, and create new curves by rewriting old curves. Everything in an L-system curve is either a forward line (denoted by Fn where n is a number representing the length of the line), or a right turn (denoted by Ra where a is an angle in degrees). We can denote left turns by using negative angles.
We create fractals by replacing all forward lines in a curve list with the original curve list. Suppose we wanted to model the growth of branches on a tree. After carefully examining the tree with our magnifying glass and industrial strength slide ruler, we discover an interesting pattern. There is a regularly repeating pattern in how the branches sprout from the trunk, and how branches grow out from yet other branches. Simplifying it as much as possible, we deduce that the pattern goes as follows: the base case (in this case the trunk of the tree) has branches at F1 O(R30 F1) F1 O(R-60 F1) F1.
This translates as: the trunk goes up one unit (in this case the numbers can represent anything form inches to feet), a branch sprouts at an angle 30 degrees to the trunk and grows for one unit. The O means an offshoot - we draw the curve in the following parentheses, and then return to where we started before the offshoot. The trunk grows another unit and now another branch, this time at -60 degrees relative to the trunk grows for one units. Finally the trunk grows for one more unit. Upon further investigation we confirm that indeed even branches follow this pattern. If we were to write this out in an organized manner we might choose to write it out as such:
Start: (F1)Here are the commands this produces after two iterations:
Rule: F1 ::= (F1 O(R30 F1) F1 O(R-60 F1) F1)
Iteration 0: (F1)
Iteration 1: (F1 O(R30 F1) F1 O(R-60 F1) F1)
Iteration 2: (F1 O(R30 F1) F1 O(R-60 F1) F1 O(R30 F1 O(R30 F1) F1 O(R-60 F1) F1) F1 O(R30 F1) F1 O(R-60 F1) F1 O(R-60 F1 O(R30 F1) F1 O(R-60 F1) F1) F1 O(R30 F1) F1 O(R-60 F1) F1)
Here's what that looks like:
 Iteration 0 |
 Iteration 1 |
 Iteration 2 |
 Iteration 5 |
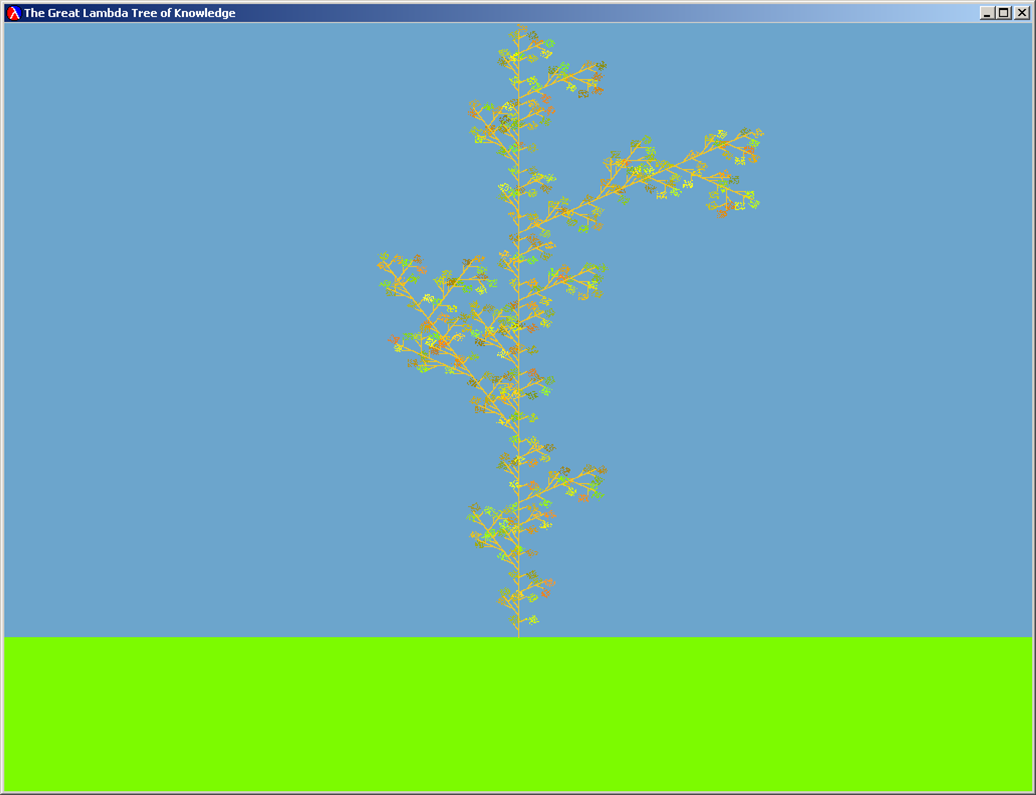 The Great Lambda Tree of Knowledge |
Note that L-system command rewriting is similar to the replacement rules in a BNF grammar. The important difference is that with L-system rewriting, each iteration replaces all instances of Fn in the initial string instead of just picking one tow replace.
We can divide the problem of producing an L-system fractal into two main parts: (1) Producing a list of L-system commands that represents the fractal by rewriting according to the L-system rule; and (2) Drawing a list of L-system commands. We'll do the drawing part first, since it will make it easier to do the fractal-producing part if we can see our fractals as pictures instead of just as lists of L-system commands. First, we consider how to represent L-system commands.
Representing L-System Commands
Here is a BNF grammar for L-system commands:
- CommandSequence ::= ( CommandList )
- CommandList ::= Command CommandList
- CommandList ::=
- Command ::= FDistance
- Command ::= RAngle
- Command ::= OCommandSequence
- Distance ::= Number
- Angle ::= Number
| Question 1: Show that (F1 O(R-60 F1) F1) is a string in the language defined by our BNF grammar. To do this, you should start with CommandSequence, and show a sequence of replacements that follow the grammar rules that produce the target string. You can use the rule numbers above to identify the rules. |
We need to find a way to turn strings in this grammar into objects we can manipulate in a Scheme program. We can do this by looking at the BNF grammar, and converting the non-terminals into Scheme objects.
;;; CommandSequence ::= ( CommandList ) (define make-lsystem-command list) ;;; We represent the different commands as pairs where the first item in the ;;; pair is a tag that indicates the type of command: 'f for forward, 'r for rotate ;;; and 'o for offshoot. We use quoted letters --- 'f is short for ;;; (quote f) --- to make tags - they evaluate to the letter after the quote. ;;; Command ::= FDistance (define (make-forward-command distance) (cons 'f distance)) ;;; Command ::= RAngle (define (make-rotate-command angle) (cons 'r angle)) ;;; Command ::= OCommandSequence (define (make-offshoot-command commandsequence) (cons 'o commandsequence))
Question 2: It will be useful to have procedures that take
L-system commands as parameters, and return information about those
commands. Define the following procedures:
|
You will find the following functions useful:
- (car lst) — evaluates to the first element of the list parameter
- (eq? v1 v2) — evaluates to #t if v1 and v2 are exactly the same; otherwise evaluates to false. For example, (eq? 's 's) evaluates to #t and (eq? 's 't) evaluates to #f.
- (error message) — produces an error with message a string given as the first parameter. For example, (error "Yikes! Attempt to get-distance for a command that is not a forward command") would display the message in red and stop execution. It is useful to use error in your code so you will more easily identify bugs.
You should be able to make up similar test cases yourself to make sure the other procedures you defined work. In lsystem.ss we define:> (is-forward? (make-forward-command 3)) #t > (is-forward? (make-rotate-command 90)) #f > (get-distance (make-forward-command 3)) 3 > (get-distance (make-rotate-command 90)) Yikes! Attempt to get-distance for a command that is not a forward command
(define (is-lsystem-command? lcommand)
(or (is-forward? lcommand)
(is-rotate? lcommand)
(is-offshoot? lcommand)))
so you should get:
> (is-lsystem-command? (make-forward-command 3)) #t > (is-lsystem-command? (list 2 3 4)) #f
Drawing an L-System Curves
Now that we have a way of representing L-System curves, we can produce procedures that display L-System curves graphically. Since we already know how to display curves represented as functions graphically from Problem Set 2, a good approach is to reuse all the work from Problem Set 2. So, to draw an L-System curve, we need a procedure that turns an L-System Curve into a function curve that maps a value between 0.0 and 1.0 to a point.Below is code for converting a list of L-System commands with some parts missing (it is explained below, but try to understand it yourself before reading further):
(define (convert-to-curve lcommands)
(if (null? lcommands)
(lambda (t) (make-point 0.0 0.0)) ; the leaves (just a point for now)
(if (is-forward? (car lcommands))
(connect-ends
(make-vertical-line (get-distance (car lcommands)))
(convert-to-curve (cdr lcommands)))
(if (is-rotate? (car lcommands))
(rotate-around-origin
;;; Question 3: fill in the first parameter to rotate-around origin
(- (get-angle (car lcommands)))
;; L-system turns are clockwise, so we need negate the angle
)
(if (is-offshoot? (car lcommands))
(connect-rigidly
;;; Question 4:
;;; fill in the first parameter to connect-rigidly
;;; fill in the second parameter to connect-rigidly
)
(error "Bad lcommand!"))))))
We are defining convert-to-curve recursively. If there are
no more commands (the lcommands parameter is null), it
evaluates to the leaf curve (for now, we just make a point - you may
want to replace this with something more interesting to make a better
fractal).
Otherwise, we need to do something different depending on what the first command in the command list is. If it is a forward command we draw a vertical line of the forward distance. The rest of the fractal is connected to the end of the vertical line using connect-ends:
(if (is-forward? (car lcommands))
(connect-ends
(make-vertical-line (get-distance (car lcommands)))
(convert-to-curve (cdr lcommands)))
The recursive call to convert-to-curve produces the
curve corresponding to the rest of the L-system commands.
| Question 3: Fill in the missing code for handling rotate commands (marked as Question 3 in the template code). |
You can test your code by drawing the curve that results from any list of L-system commands that does not use offshoots. For example, evaluating
should produce a "V".(draw-curve-points (translate (convert-to-curve (make-lsystem-command (make-rotate-command 150) (make-forward-command .5) (make-rotate-command -120) (make-forward-command 0.5))) 0.3 0.7) 10000)
| Question 4: Fill in the missing code for handling offshoot commands (marked as Question 4 in the template code). |
We have provided a procedure to make it easier to fit fractals onto the graphics window:
- (position-curve curve startx starty) — evaluates to a curve that translates curve to start at (startx, starty) and scales it to fit into the graphics window maintaining the aspect ratio (the x and y dimensions are both scaled the same amount)
Now, you should be able to draw any l-system command list using position-curve and the convert-to-curve function you completed in Questions 3 and 4. Try drawing a few interesting L-system command lists before moving on to the next part.
Rewriting Curves
The power of the L-System commands comes from the rewriting mechanism. Recall how we described the tree fractal:Start: (F1)To produce levels of the tree fractal, we need a procedure that takes a list of L-system commands and replaces each forward command with the list of L-system commands given by the rule.
Rule: F1 ::= (F1 O(R30 F1) F1 O(R-60 F1) F1)
So, for every command in the list:
- If the command is a forward command, replace it with the replacement commands
- If the command is a rotate command, keep it unchanged
- If the command is an offshoot command, recursively rewrite the every command in the offshoot's command list the same way
For example, consider a simple L-System rewriting:
Start: (F1)We want to get:
Rule: F1 ::= (F1 R30 F1)
Iteration1: (F1 R30 F1)but if we just replace F1's with (F1 R30 F1) lists, we would get:
Iteration2: (F1 R30 F1 R30 F1 R30 F1)
Iteration1: ((F1 R30 F1))The easiest way to fix this problem is to flatten the result. Here's how (this code is provided in lsystem.ss:
Iteration2: ((F1 R30 F1) R30 (F1 R30 F1))
(define (flatten-commands ll)
(if (null? ll) ll
(if (is-lsystem-command? (car ll))
(cons (car ll) (flatten-commands (cdr ll)))
(flat-append (car ll) (flatten-commands (cdr ll))))))
(define (flat-append lst ll)
(if (null? lst) ll
(cons (car lst) (flat-append (cdr lst) ll))))
|
Question 5: Define a procedure rewrite-lcommands that
takes a list of L-system commands as its first parameter. The second
parameter is a list of L-system commands that should replace every
forward command in the first list of commands in the result.
Here's the easy part: Complete the definition of rewrite-lcommands.(define (rewrite-lcommands lcommands replacement) (flatten-commands (map ; Procedure to apply to each command lcommands))) |
|
Question 6: Define a procedure make-lsystem-fractal that
takes three parameters: replace-commands, a list of L-system
commands that replace forward commands in the rewriting; start,
a list of L-system commands that describes the starting curve;
level, the number of iterations to apply the rewrite rule.
Hint: the n-times function you defined in PS2 might be useful. |
You should be able to draw a tree fractal using make-tree-fractal and draw-lsystem-fractal (these and the tree-commands list of L-system commands are defined in lsystem.ss):
(define (make-tree-fractal level) (make-lsystem-fractal tree-commands (make-lsystem-command (make-forward-command 1)) level)) (define (draw-lsystem-fractal lcommands) (draw-curve-points (position-curve (convert-to-curve lcommands) 0.5 0.1) 50000))
| Question 7: Draw some fractals by playing with the L-system commands. Try changing the rewrite rule, the starting commands, level and leaf curve (in convert-to-curve) to draw an interesting fractal. Turn in the code you used, as well as a printout of the display window. |
Better Drawing
Everything beyond here is optional, but makes it possible to draw better fractals with only a little more work.The problem we observe in Problem Set 2 with our connect-curve-rigidly (and also connect-ends) not distributing the t values well is much worse for our L-system fractals.
If we draw (make-tree-fractal 5), it has 1707 different curves! The way connect-ends is defined, we use t-values 0.0 through 0.5 all on the first curve, and 0.5 through 1.0 on the other 1706 curves. This procedure evaluates to the approximate number of points for the nth curve:
Evaluating (exact->inexact (num-points 100000 100)) produces 7.888609052210118e-026 meaning there is less than 1 in 1025 chance that a single point from the 100th curve is drawn!(define (num-points p n) (if (= n 0) p (num-points (/ p 2) (- n 1))))
To fix this, we need to distribute the t-values between our curves in a more sensible way. We have provided a procedure connect-curves-evenly in curves.ss that connects a list of curves in a way that distributes the range of t values evenly between the curves. Its a bit complicated, but you should be able to understand its definition:
(define (get-nth list n)
(if (= n 0) (car list) (get-nth (cdr list) (- n 1))))
;;; Divide t evenly among a list of curves
(define (connect-curves-evenly curvelist)
(lambda (t)
(let ((which-curve
(if (>= t 1.0) (- (length curvelist) 1)
(inexact->exact (floor (* t (length curvelist)))))))
((get-nth curvelist which-curve)
(* (length curvelist)
(- t (* (/ 1 (length curvelist)) which-curve)))))))
To use this to draw better L-system fractals, you will need to replace
your convert-to-curve procedure with a
convert-to-curve-list procedure that keeps all the curves separate instead of connecting them directly. Then,
will produce a nice tree fractal. You have to write the convert-to-curve-list code yourself, but don't hesitate to ask for help if you are stuck on this.(define (draw-lsystem-fractal lcommands) (draw-curve-points (position-curve (connect-curves-evenly (convert-to-curve-list lcommands)) 0.5 0.1) 50000))
| Credits: This problem set was created by Dante Guanlao, Jon Erdman and David Evans. |
