| Exam 2 |
Out: 18 April 2003 Due: Wednesday, 23 April 2003, 2:00PM |
|
|
Work alone. You may not discuss these problems or anything related to them with anyone except for the course staff between receiving this exam and class Wednesday. You may send email to cs200-staff@cs.virginia.edu to ask for clarifications on what the questions mean. You may (and should) continue to work with your PS8 team on your PS8 project, but avoid discussing anything closely related to the exam.Open book. You may use any books you want, lecture notes and slides, your notes, and problem sets. If you use anything other than the course books and notes, cite what you used. If you want, you may use DrScheme, but you are not expected to test real code for any of these questions.
Closed web. You may not search the web for material relevant to this problem set.
Halt. Don't spend an unreasonable amount of time on this exam. There is no set time limit, but you should not spend more than a few hours on the exam. If you get stuck, move on to the next question.
Answer well. Answer all 10 questions. Write your answers in the spaces provided in this exam. If you need more space (you shouldn't), you may use the backs of pages. If you prefer to type your answers, you may turn in your own sheets but make sure your answers are clearly marked.
Full credit depends on the clarity and elegance of your answer, not just correctness. Your answers should be as short and simple as possible, but not simpler.
Mutation and Objects
Consider the classes defined below: sail-boat is a subclass of boat which is a subclass of object.
(define (ask object message . args)
(apply (get-method object message) object args))
(define (get-method object message)
(object message))
(define make-object
(lambda (name)
(lambda (message)
(case message
((class) (lambda (self) 'object))
((object?) (lambda (self) #t))
((name) (lambda (self) name))
(else (error "No method"))))))
(define make-boat
(lambda (name)
(let ((super (make-object name))
(floating #t))
(lambda (message)
(case message
((class) (lambda (self) 'boat))
((boat?) (lambda (self) #t))
((is-floating?) (lambda (self) floating))
((sink) (lambda (self) (set! floating #f)))
(else (get-method super message)))))))
(define make-sail-boat
(lambda (name)
(let ((super (make-boat name))
(sailing #f))
(lambda (message)
(case message
((class) (lambda (self) 'sail-boat))
((raise-sail) (lambda (self) (set! sailing #t)))
((lower-sail) (lambda (self) (set! sailing #f)))
(else (get-method super message)))))))
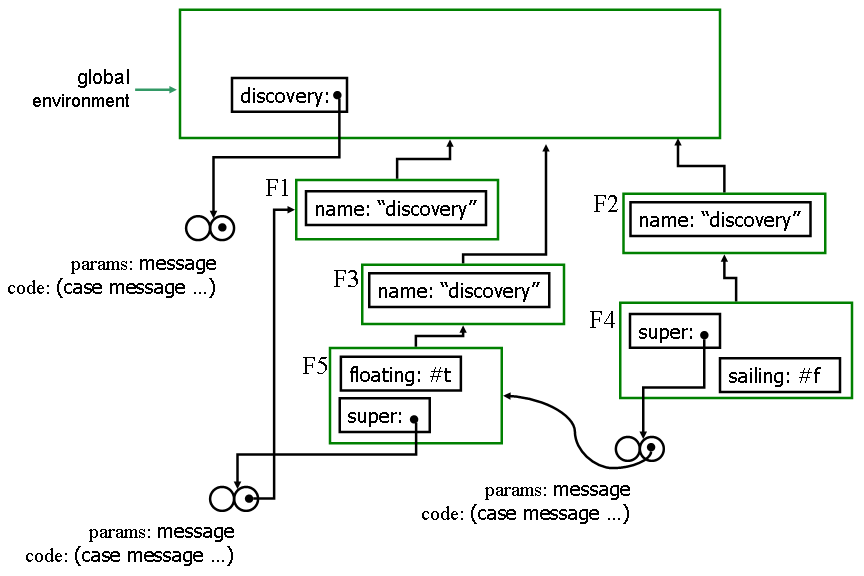
1. The following environment diagram shows the state after
evaluating (define discovery (make-sail-boat "discovery")).
The procedure associated with the name discovery is missing
its environment pointer. Add the missing environment pointer to the
diagram.
2. There are three frames in the diagram (labeled F1, F2 and F3) that contain a place named name with the value "discovery". If we evaluate (ask discovery 'name) in the global environment, in which frame with the value of name be found?
|
|
Metalinguistics
I. M. Perative is upset that Mini-Scheme does not contain her favorite control structure repeatuntil. I. M. doesn't understand recursive definitions, but really likes mutation. She wants to write a procedure that computes the length of a list like this:
(define (length lst)
(let ((len 0))
(repeatuntil
(null? lst)
(begin
(set! lst (cdr lst))
(set! len (+ 1 len)))
len)))
repeatuntil takes three operands. If evaluating the first
operand produces a false value, then the second operand is evaluated,
and the repeatuntil is evaluated again. It will keep
evaluating like this until the first operand produces a true value.
If evaluating the first operand produces true, then the third operand
is evaluated and its value is the value of the repeatuntil
expression. Hence, the length procedure above will evaluate
to the length of the list. The repeatuntil expression will
evaluate its second operand,
(begin (set! lst (cdr lst)) (set! len (+ 1 len))) repeatedly
until (null? lst) is true. Hence, it will evaluate the
second operand one time for each element in lst, and
increment the value of len once for each element. Then, it
will evaluate to the value of the third operand, len.
3. Explain why I. M. will not be able to define repeatuntil as a procedure herself in Mini-Scheme, but must instead change the evaluator.
|
|
4. I. M. has asked you to extend Mini-Scheme to support repeatuntil. Provide the missing definition for eval-repeatuntil. The new code is shown below; you may assume everything else from PS7's meval is available.
Note: You are not forbidden from trying out your code in DrScheme, but you are not expected to do so (and we are not providing code to download to discourage you from doing this). We hope you are confident enough to answer this question without needing to test your code. You will not lose points for unimportant mistakes (like miscounting parentheses) that you would notice easily by testing your code. Please do not spend huge amounts of time trying to solve this using "trial-and-error" programming!
(define (meval expr env) (cond ((self-evaluating? expr) expr) ((quoted? expr) (text-of-quotation expr)) ((definition? expr) (define-variable! (definition-variable expr) (meval (definition-value expr) env) env)) ((lambda? expr) (make-procedure (lambda-parameters expr) (lambda-body expr) env)) ((repeatuntil? expr) (eval-repeatuntil expr env)) ((application? expr) (mapply (meval (application-operator expr) env) (map (lambda (subexpr) (meval subexpr env)) (application-operands expr)))) ((variable? expr) (environment-lookup-name expr env)) ;; Must be last (else (error "Unrecognized expression: " expr)))) (define (repeatuntil? expr) (tagged-list? expr 'repeatuntil)) (define (repeatuntil-test expr) (cadr expr)) (define (repeatuntil-body expr) (caddr expr)) (define (repeatuntil-result expr) (cadddr expr))
(define (eval-repeatuntil expr env) ) |
Problems about Problems
For problems 5-7, classify each problem as decidable or undecidable. If the problem is undecidable, explain convincingly why there is no algorithm that solves it. A convincing argument would show how you can use a solution to the given problem to solve a problem you already know is undecidable.If the problem is decidable, describe the complexity of the problem using O (upper bound) and Ω (lower bound). Either provide a tight bound (Θ) or explain why you cannot provide a tight bound. Support your answers with convincing arguments. A good answer should describe a procedure that solves the problem to justify your upper bound, and identify a minimum amount of work necessary to justify your lower bound. Correctness is most important, but for full credit your answers should be as precise as possible.
5. Minimum Value Problem. Find the smallest value in a list.
Input: A non-empty list of n numbers.
Output: The smallest (using < to compare numbers) number in the input list.
|
|
Input: A program P and input n
Output: If evaluating P applied to n would produce a value greater than 0, true. If evaluating P applied to n would produce a value that is not a number, or is a number less than or equal to 0, or would not terminate, output is false.
|
|
7. Many Goldstars Problem. The input tape is n star symbols followed by the end of tape symbol. The output tape is 2n star symbols followed by the end of tape symbol.
Input: n stars
Output: 2n stars
|
|
Lambda Calculus
In class, we defined if, T and F using Lambda Calculus as:if ≡ λ pca . p c aSuppose we instead defined if as:
T ≡ λ xy . x
F ≡ λ xy . y
if ≡ λ pca . p a c8. Show how T and F would need to be defined to make the new definition of if work correctly.
|
|
Universal Language
Consider the preSQL language described below:Commands ::= Command ; CommandsPreSQL is similar to SQL except:
Commands ::= Command
Command ::= CreateTableCommand | InsertCommand | CountCommand | DeleteCommand
CreateTable ::= CREATE TABLE Name
Create a new table named Name with no entries.
InsertCommand ::= INSERT INTO Table Value
Insert a value (TRUE or FALSE) as the last element in table Table.
Value ::= TRUE
Value ::= FALSE
CountCommand ::= COUNT Table
Evaluates to the number of entries in Table.
DeleteCommand ::= DELETE FROM Table
Remove the first (earliest inserted) element from the table Table.
- Entries in a table have one value (TRUE or FALSE). There are no fields, since each table entry is only one value. (Note that there is no way to get the actual values of entries.)
- The DELETE command just deletes the first entry in the table.
- There is no SELECT command and no UPDATE command.
- The COUNT command can be used to obtain the number of entries in a table.
9. Is PreSQL a Universal Language? Use convincing arguments to support your answer.> CREATE TABLE tab
> INSERT INTO tab TRUE
> INSERT INTO tab FALSE
> COUNT tab
2
> DELETE FROM tab
> COUNT tab
1
|
|
Command ::= UNTILEMPTY Table { Commands }UNTILEMPTY will check if Table is empty (that is, it has zero entries). If it is empty, it does nothing. Otherwise, it will execute the Commands and repeat the UNTILEMPTY command. It will keep repeating the Commands until the Table is empty.
For example, UNTILEMPTY tab { DELETE FROM tab } would delete all entries from that table tab.
10. Show how you could do addition using PreSQLsql. Your addition code should assume the input is in the form of two tables, tableA and tableB. After addition, a new table named output should have the result. Provide code that could be used for the missing code below that would correctly add any two natural numbers (your code may modify the input tables):
|