|
This is the final from last year. Your final may be quite different
from this in format and content. This is being provided to give you
some practice questions to prepare for Exam 2.
We have not yet covered all the material that is on this exam (questions 9 and 10), but we will cover it before Exam 2. We recommend you try the exam yourself before looking at the answers. You can see the answers at http://www.cs.virginia.edu/evans/cs200-spring2002/exams/final-answers.html. |
| Final Exam |
Out: 29 April 2002 Due: Monday, 6 May 2002, 5:00 PM (turn in your exam at Olsson 236A) |
Procedures
1. Define a procedure increment-list that takes a list of numbers, and produces a new list of numbers with each number incremented by one. For example, (increment-list (list 2 0 0 88)) should evaluate to the list (3 1 1 89). Do not use map in your definition.2. Use map to define increment-list as in question 1.
3. Define a procedure make-traced-procedure that can be used to observe applications of another procedure. Your make-traced-procedure should work like this:
Note that the traced procedure is only evaluated once (for each time it would be evaluated if it were not traced). You may use (display (list "Result: " val)) to print out the string "Result:" and the value val.> (define double (make-traced-procedure (lambda (x) (printf "in double~n") (+ x x))))
> (map double (list 1 2 3))
Called procedure
in double
(Result: 2)
Called procedure
in double
(Result: 4)
Called procedure
in double
(Result: 6)(2 4 6)
Objects and Environments
Cy D. Fect defines a procedure reverse! that uses mutation to reverse a list:
(define (next-to-last-pair lst)
(if (null? lst) (error "Null list!")
(if (null? (cdr lst)) (error "Single length list!")
(if (null? (cdr (cdr lst))) lst
(next-to-last-pair (cdr lst))))))
(define (reverse! lst)
(if (or (null? lst) (eq? 1 (length lst)))
#f ;; Nothing to do for empty or length 1 list (value doesn't matter)
(let* ((nexttolast (next-to-last-pair lst))
(lastpair (cdr nexttolast))
(first (car lst)))
;;; Point 0
(set-cdr! nexttolast null)
;;; Point 1
(reverse! (cdr lst))
(set-cdr! nexttolast lastpair)
(set-car! lst (car lastpair))
;;; Point 2
(set-car! lastpair first))))
Consider evaluating:
> (define ilist (list 1 2 3))
> (reverse! ilist)
> ilist
(3 2 1)
At Point 0 on the first call to reverse! the environment looks like:
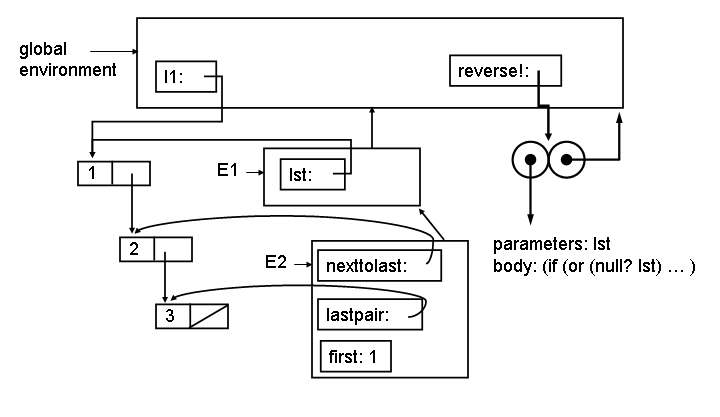
The E1 environment is created by the application (reverse! ilist). The E2 environment is created by the let inside reverse! (which desugars to an application of a lambda). (The let* actually desugars into more than one lambda, and more than one environment, but for this question we combine them into one environment.)
4. Show what the environment looks like at Point 1 (after evaluating (set-cdr! nexttolast null)). To make your drawing easier, here is a template drawing. You can answer this question by only adding to this template.
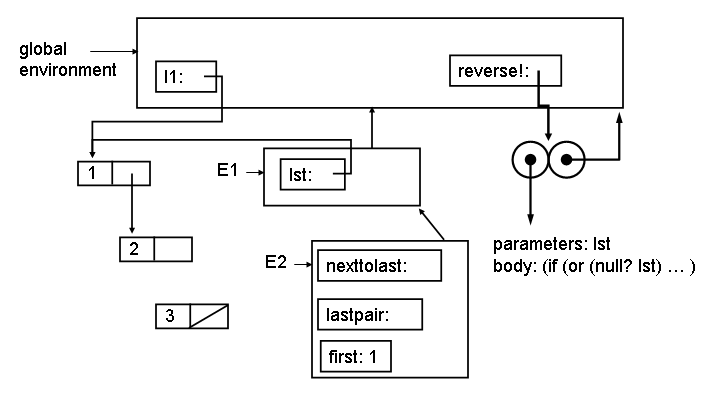
|
5. Show what the environment looks like at Point 2. You can answer this question by only adding to this template.
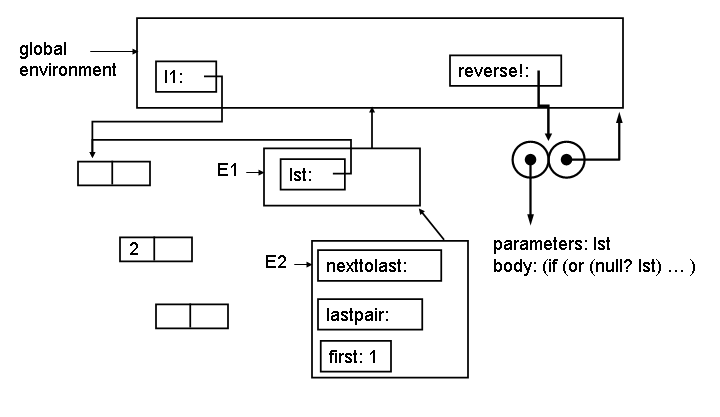
|
Turing Machines
6. The Turing Machine for checking balanced parentheses from Lecture 34 was incorrect. In particular, it would incorrectly report balanced parentheses for input such as ((). Correct the Turing Machine so it correctly ends with 1 at the tape head if the parentheses are balanced, and 0 otherwise. You should only need to add 1 state to the Turing Machine below:
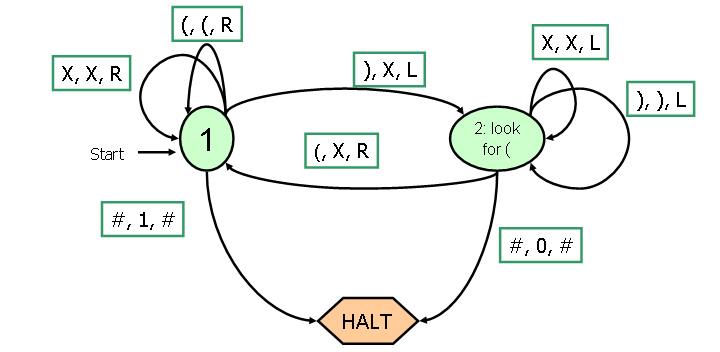
Lambda Calculus
7. Given T, F and if as defined in class:T ≡ λ x (λ y . x)a. Define a Lambda Calculus term that behaves like not. For example, if (not T) M N should reduce to N and if (not F) M N should reduce to M.
F ≡ λ x (λ y . y)
if ≡ λ pca . pca
b. Show that your definition of not works by showing the steps to reduce if (not T) M N to normal form (where M and N represent and Lambda Calculus term in normal form).
Models of Computation
Phine Knight suggests the modelling computation using a Phine Machine consisting of a list of numbered instructions (the Instructions), a pointer to the current instructions (the InstructionPointer), and a store that associates name and values (the Store).A program executes by executing the instruction numbered by the InstructionPointer, and then increasing the InstructionPointer by 1. This continues unless the Instruction is HALT.
Instructions can do one of four things:
- Set the value associated with a name to zero (e.g., X := 0)
- Set the value associated with a name to the value of a name plus 1 (e.g., Y := X - 1)
- Set the value associated with a name to the value of a name minus 1 (e.g., X := X - 1)
- Halt (e.g., HALT)
( <1: X := 0
2: X := X + 1
3: Y := X - 1
4: HALT >,
1,
{ } )
The model will start by executing instruction number 1, which puts <X,
0> in the store and advances the Instruction Pointer to 2.
After this, the state is:
( <1: X := 0
2: X := X + 1
3: Y := X - 1
4: HALT >,
2,
{ <X, 0> } )
After the next two steps, the state will be:
( <1: X := 0
2: X := X + 1
3: Y := X - 1
4: HALT>,
4,
{ <X, 1>, <Y, 0> } )
8. Write a BNF grammar that could be used to describe the state
of a Phine Machine. A good answer will describe the smaller language
possible that includes strings for describing all possible Phine
Machine states.
9. Is this Phine Machine model of computation equivalent to a Turing Machine? Argue convincingly why it is or isn't.
10. Condy Shonal suggests adding one new instruction to Knight's model:
Instruction ::= IF Name = 0 GOTO Number
If the value of Name in the Store is 0, then this instruction sets
the InstructionPointer to Number. If it is not, then this instruction
does nothing and advances the InstructionPointer by one.
For example,
( <1: IF A = 0 GOTO 5
2: B := B + 1
3: A := A - 1
4: GOTO 1
5: HALT>,
1,
{ <A, n>, <B, m> } )
is a program that will halt with B having the value n + m.
Condy claims her new model of computation is as powerful as a Turing Machine, but Fine Knight does not believe her. Write an informal but convincing argument that this model is as powerful as a Turing Machine.
