CS200: Notes 9 April 2003

University of Virginia, Department of Computer Science
CS200: Computer Science, Spring 2003

Notes: Wednesday 9 April 2003

Schedule

Today: sign up for Design Reviews
Friday, 11 April, 11:00 am: Christopher Frost and Michael Peck, Pancakes, Puzzles and Polynomials: Cracking the Cracker Barrel Game. UVa Research and Design Symposium, Jefferson Hall (note location change).
Friday, 18 April: Exam 2 out
Wednesday, 23 April: Exam 2 Due
28 April (9am): Problem Set 8 Due

Design Reviews
You should come to your design review prepared to answer these questions:

If your project is successful, what will your site do on April 28?
If your project is successful, what will your site be like in April 2005?
How will you divide the work amongst your team?
How will you manage your team?
What is the hardest technical problem you have to solve to make your project successful?
What ideas do you have for solving that problem?
Models of Computation
What is a model?

What do we need to model computation?

Finite State Machine

FSM ::= <Alphabet, States, InitialState, HaltingStates, TransitionRules>
Alphabet ::= { Symbol^* }
    A set of symbols for the input.
States ::= { StateName^* }
InitialState ::= StateName
    Must be one of the states in States.
HaltingStates ::= { StateName^* }
    Must all be states in States.
TransitionRules ::= { TransitionRule^* }
TransitionRule ::= < StateName, Symbol, StateName>
    StateName X Symbol → StateName

Turing Machine

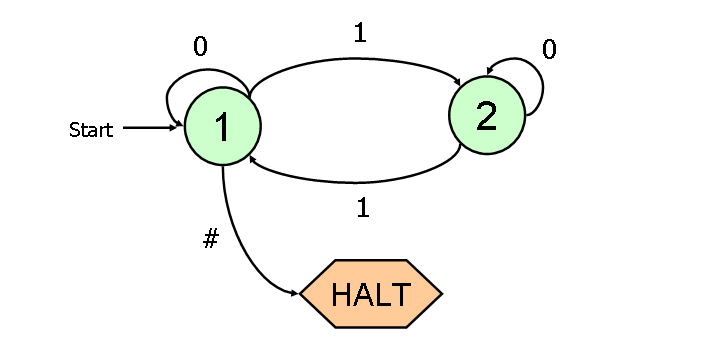
TM ::= <Alphabet, Tape, TFSM>

Alphabet ::= { Symbol^*}
    A set of symbols for the tape.

Tape ::= < LeftSide, OneSquare, RightSide >
OneSquare ::= Symbol | #
LeftSide ::= [ Squares^* ]
    Everything to left of LeftSide is #. RightSide ::= [ Squares^* ]
    Everything to right of RightSide is #. Squares ::= OneSquare, Squares
Squares ::=
TFSM ::= <States, InitialState, HaltingStates, TransitionRules>
    Like a FSM, except the transition rules write to the tape and move the tape head.
States ::= { StateName^* }
InitialState ::= StateName    Must be one of the states in States.
HaltingStates ::= { StateName^* }    Must all be states in States.
TransitionRules ::= { TransitionRule^* }
TransitionRule ::= < StateName, OneSquare, StateName, OneSquare, Direction>
    StateName X OneSquare → StateName X OneSquare X Direction

Universal Turing Machine
A Turing Machine that can simulate any other Turing Machine on an input: TM_U (P, I) = the output of running TM-P on input I

Links

Alan Turing site by Andrew Hodges, author of Alan Turing: the Enigma (Douglas Hofstadter wrote the preface)
Manchester Illuminated Universal Turing Machine (Turing Machine Art)
HTML is not a univeral language, but XSLT style sheets are: universal turing machine implemented using XSLT
Universal Turing Machine print (title slide picture)
Turing Machines (animations)








	CS 200: Computer Science Department of Computer Science University of Virginia Circle Fractal by Ramsey Arnaoot and Qi Wang	cs200-staff@cs.virginia.edu Using these Materials