[an error occurred while processing this directive]

<center><h2>Section 2 Notes</h2></center>


    <h2>Lists</h2>

    What are possible representations for lists?
    <br><br><br><br><br><br>

    How would you implement list operations for different representations
    of a list?
<p>

    <table border="1" width="100%">
      <tr>
	<th width="100px">Operation</th>
	<th width="40%">Linked List</th>
	<th>Continuous</th>
      </tr>
      <tr>
	<td>Append(L, e)<br><br><br><br><br><br><br></td>
	<td>&nbsp;</td>
	<td>&nbsp;</td>
      </tr>
      <tr>
	<td>Remove(L, e)<br><br><br><br><br><br><br></td>
	<td>&nbsp;</td>
	<td>&nbsp;</td>
      </tr>
      <tr>
	<td>GetPosition(L, e)<br><br><br><br><br><br></td>
	<td>&nbsp;</td>
	<td>&nbsp;</td>
      </tr>
      <tr>
	<td>Find(L, e)<br><br><br><br><br><br><br><br></td>
	<td>&nbsp;</td>
	<td>&nbsp;</td>
      </tr>
    </table>

<p class="page"></p>

    <h2>Trees</h2>
    What are the different types of trees?
    
    <br><br><br><br><br><br><br>

    <h3>Tree terminology</h3>
    <ul>
      <li>A <b>leaf</b> has no children.</li>
      <li><b>Siblings</b> have the same <b>parent</b>.</li>
      <li>A <b>path</b> is a sequence of nodes n<sub>1</sub>, n<sub>2</sub>, ..., n<sub>k</sub> such that 
      n<sub><em>i</em></sub> is the parent of n<sub><em>i</em>+1</sub>
      <li>The <b>length</b> of a path is the number of edges in the path.</li>
      <li>The <b>depth</b> of a node is the length of the path from the root to 
      the node.</li> 
      <li>The <b>height</b> of a tree is the length of the longest path from 
      root to a leaf.</li>
    </ul>
<!--
    <br><br>

    <img src="nonbinary.png"><br>
    A generic tree<br><br><br>

    <img src="numb_deleteRootgiven.png"><br>
    A binary tree<br><br><br>

    <img src="calculate.png"><br>
    A tree that represents a mathematical expression. <br> <b> What value does the above tree give? </b><br><br>
-->

    <h2>Questions</h2>

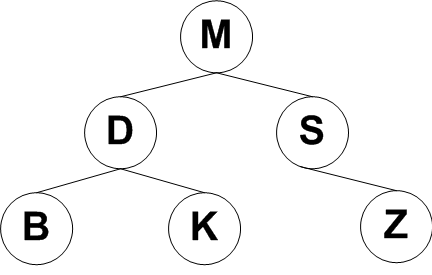
    <b>1.</b> Insert G, H, F, and O into the alphabetically sorted binary tree below:<br>
<p>
    <img src="insertGgiven.png">
<p class="page"></p>
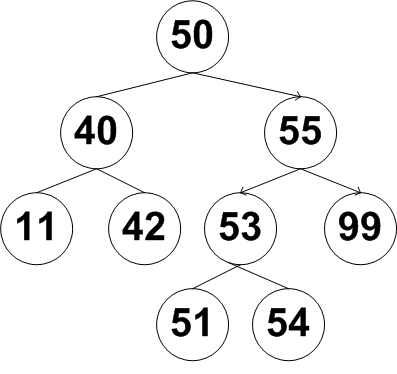
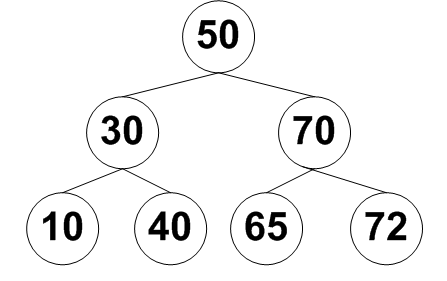
   <b>2.</b> Insert 30 into the numerically sorted binary tree below:<br>
<p>
 <img src="Insert30-agiven.png"><br>
<p>
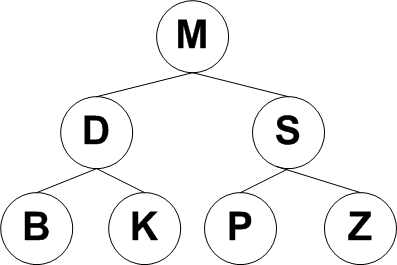
  <b>3.</b> Delete P from the alphabetically sorted binary tree below:<br>
<p>
      <img src="deletePgiven.png"><br>
<p class="page"></p>
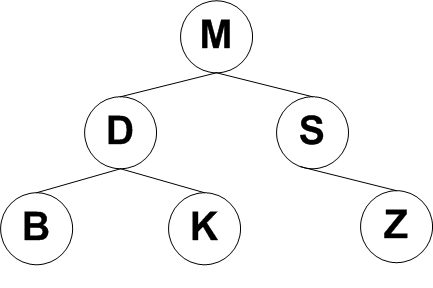
  <b>4.</b> Delete D from the alphabetically sorted binary tree below (show all
 possibilities):<br>
<p>
    <img src="deleteDgiven.png"><br>
<p>
    <b>5.</b> Delete the root (show all possibilities that preserve a sorted
    binary tree):<br>
<p>
    <img src="numb_deleteRootgiven.png"><br>
<p class="page"></p>

    <h2>Running Time</h2>
    <table border="1" cellpadding=12>
      <tr>
	<th>Operation</th>
	<th>Linked List</th>
	<th>Continuous List</th>
	<th>Sorted Binary Tree</th>
      </tr>
      <tr>
	<td>Insert(L, index, x) for lists<br>
	  Insert(T, x) for trees<br><br></td>
	<td>&nbsp;</td>
	<td>&nbsp;</td>
	<td>&nbsp;</td>
      <tr>
	<td>Find(L, x)<br><br></td>
	<td>&nbsp;</td>
	<td>&nbsp;</td>
	<td>&nbsp;</td>
      </tr>
      <tr>
	<td>Remove(L, x)<br><br></td>
	<td>&nbsp;</td>
	<td>&nbsp;</td>
	<td>&nbsp;</td>
      </tr>
    </table>

    <br><br>

    Draw all the binary trees that you can generate with this set 
    of data (Hint: Try inserting in different orders):<br>
    1, 3, 5, 7<br>

<p><br><p><br><p><br><p><br><p><br><p><br><p><br>


[an error occurred while processing this directive]