Problem Set 3: Public-Key Cryptosystems

Selected Answers

Average: 84.5/100
Problem 1: 17.8 (15 + 20)
Problem 2: 14.4 (15)
Problem 3: 23.8 (30 + 15)
Problem 4: 7.2 (10)
Problem 5: 21.2 (30)

1. Key Distribution

Recall the Keys "R" Us distribution scheme from Lecture 6: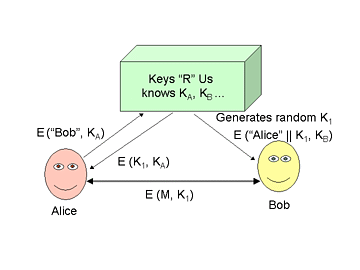 The protocol is:

1. Alice meets securely with Keys "R" Us and agrees on secret key K_A
2. Bob meets securely with Keys "R" Us and agrees on secret key K_B
3. Alice sends E ("Bob", K_A) to Keys "R" Us
4. Keys "R" Us generate a new, random key: K₁
5. Keys "R" US sends Alice, E (K₁, K_A); Alice decrypts using K_A to get K₁.
6. Keys "R" US sends Bob, E ("Alice" || K₁, K_B); Bob decrypts using K_B to get K₁.
7. Alice and Bob communicate using shared secret key K₁.

a. (15) One of the problems with the Keys "R" Us protocol is the trusted third party can eavesdrop on all communications between Alice and Bob since Keys "R" Us knows K₁. Suggest a modification to the scheme that solves this problem.

Your solution should satisfy these requirements:

1. Alice and Bob agree on a secret key, K₁, without ever meeting.
2. Alice and Bob can be assured they are communicating with each other.
3. No one besides Alice and Bob (including (semi-) trusted parties and eavesdroppers) can obtain any information about K₁. You may assume there is a perfect encryption function E (m, k), and that independent semi-trusted third do not conspire together.
4. Your scheme must not use exponentiation or modulo arithmetic. (It shouldn't be based on a public-key cryptosystems we have seen.)

Alice and Bob may meet securely with (hint: one or more) trusted third parties at the beginning of the protocol.

Answer: With two trusted third parties it is simple. Alice and Bob each establish secret keys with Keys "R" Us and eKeys. Alice and Bob use the original protocol to establish K1 through Keys "R" Us, and use the original protocol through eKeys to establish K2. Alice and Bob communicate securely using K = K1 XOR K2. Neither Keys "R" Us nor eKeys can independently decode the messages.

b. (up to 20 bonus points) Since Alice and Bob are having an illicit affair (its a cyber affair, so they still cannot meet in person to exchange keys), not only do they want their messages to be private, they don't want anyone else to know they are even communicating with each other. Once they have obtained a secret key, this is easy: Alice posts her encrypted message in a public place where Bob knows to look (for example, they can place classified ads in the New York Times).

Adapt your solution to (a) to meet the additional requirement that no one (including trusted parties) can know Alice and Bob are communicating with each other. The other requirements should still hold, including Alice and Bob still obtain a shared secret key, and Alice should be confident she is communicating with Bob and vice versa.

Answer: Without using public-key techniques, this is much harder.

One approach (Aaron Bajek and GJ Halfond suggested schemes similar to this, but vulnerable to traffic analysis) is to give each person a bit string identifier (e.g., Alice is 10010, Bob is 01011). There must be enouch people in the system so that most bit-strings are used. If the bit-string are 5-bits long, there should be 32 people in the system, and an attacker should have no better than 1/31 chance of guessing who Alice is having an affair with (this assumes she isn't having an illicit affair with herself).

To establish secret communication with Bob, Alice sends "0xxxx" to a randomly-choosen trusted party (the more trusted parties there are the more secure the scheme is; ideally, there should be one per ID bit). The trusted party creates two random keys, K_0 and K_0x, and sends K_0 to each person whose ID starts with 0 (encrypted with the shared secret key each individual has with the trusted third party). The trusted party sends K_0x to every person whose ID starts with 1. This is a decoy message, but necessary if we want to be secure against traffic analysis attacks. If the trusted third party didn't send this out, an attacker could monitor all the traffic on the network and know that Alice wants to communicate with someone whose ID starts with 0. The trusted third party also send Alice K_0 encrypted with the secret key shared between Alice and the trusted third party. (Because K_0 is encrypted, an eavesdropper cannot tell if Alice was sent K_0 or K_0x).

Next, Alice sends "x1xxx" to a different randomly-choosen semi-trusted party. This party generates K_1 and K_1x, and sends it out according to the same protocol as the first trusted party used for K_0. The process continues through each ID bit.

At the end of the process, Alice and Bob both have K_0, K_1, ..., K_n. They calculate K = K_0 XOR K_1 XOR ... XOR K_n and use this as the secret key for communication. No semi-trusted third party knows more than one bit of the ID, so they have at best a 1 in n/2 chance of guessing with whom Alice is communicating.

Alice knows she is really communicating with Bob, because only Bob recieves all the components of K. Bob, however, does not know he is really communicating with Alice. One easy (but expensive) way he could authenticate this is to do the process in reverse where he is the one how initiates the communication. This produces a new key K'. If they communicate using K XOR K', both Alice and Bob know they are communicating with the right person.

Using public-key protocols, we can accomplish the same thing with considerably less effort. Alice just encrypts her message using Bob's public key and posts it in the newspaper. Only Bob can read it (using his private key), and no one else can tell the message is between Alice and Bob. If she also encrypts it using her private key, Bob can authenticate that the message came from Alice using her public key. (Later, we will see some examples of anonymous email and web browsing that provide similar anonymity to newspaper classified over the Internet. We can do this by sending messages along a chain of randomly choosen forwarding servers, with the next destination encrypted using the next server's public key.)

2. Primal Tendancies

In the RSA paper, the authors claim that it is okay to use a probablistic prime number test since if a composite number is choosen the receiver would probably detecte it by noticing that decryption didn't work correctly.

That is, choosing a composite number is not likely to lead to a substantial security flaw, since the problem would be detected in the first transmission. Note that if it were not detected, choosing a composite number for p or q would be bad, because an attacker would have an easier time factoring n = p * q = (p₁ * p₂) * q since one of the p factors is small (around sqrt (sqrt (n))).

a. (10) Illustrate that decryption doesn't work if the choosen p is composite using an example. That is, pick p, q, e and d consistent with the RSA algorithm except p is composite, and show for some M: D (E (M)) ¹ M.

Answer: Here is an example (based on Dave Rubens' answer):

p = 4, q = 7
n = 28
Phi(n) = (p - 1) (q - 1) = 18

e = 11      gcd(11,18) = 1 so e is valid.
d = 5       e * d = 55 == 1 mod 18

M = 2
E (M) = M^e mod n = 2048 mod 28 = 4
D (4) = C^d mod n = 4⁵ mod 28 = 1024 mod 28 = 16

So, D (E (M)) is not equal to M, and RSA breaks when we choose composite p.

b. (5) Show how the proof that D (E (M)) = M breaks if p is composite. (You don't need to reproduce a complete proof, just identify the step of the proof that depends on p being prime.)

Answer:

The proof breaks becase the totient function equality depends on n being prime:

If n is prime, (n) = n - 1.

If n is composite, this is not true.

3. Public-Key Poker

Alice, Bob and Colleen Hacker want to play poker on the Internet. A playing card deck has 52 cards. They agree to identify each card using a number:

   suit = 0 | 1 | 2 | 3 (hearts, clubs, diamonds, spades)
   number = 1 (Ace) | 2 | 3 | ... | 10 | 11 | 12 | 13 
   cardid = (13 * suit) + number

so the queen of diamonds is card 26 + 12 = 38.

Play proceeds as follows:

1. Alice, Bob and Colleen each generate RSA public-private key pairs: KU_A (Alice's public key), KR_A (Alice's private key); KU_B, KR_B; KU_C, KR_C. The public keys KU_A, KU_B, KU_C are securely published.
2. Alice generates a "deck" of 52 cards, encrypts all cards with KU_A. She sends all the cards in random order to Bob.
3. Bob encrypts all cards with KU_B, and sends the cards in random order to Colleen.
4. Colleen encrypts all the cards with KU_C, and sends the cards in random order to Alice. At this point, the card m is encrypted as E_KUC [E_KUB [E_KUA [m]]]].
5. Alice chooses five cards, and sends the remaning 47 cards to Bob (and keeps a copy of them for himself).
6. Bob chooses five cards from the cards Alice sent, and sends the remaning 42 cards to Colleen (and keeps a copy of them for himself).
7. Colleen chooses five cards from the cards Bob sent, and sends the remaining 37 cards to Alice.
8. Each player publishes their private keys. The all decrypt their cards and reveal their hands. Each player also decrypts the cards they passed to the next player to make sure no one cheated.

a. (10) Alice and Bob are subject to the UVA Honor Code, but Colleen has no such scruples. After Colleen gets royal flushes (the best poker hand) for the first few hands, Alice and Bob begin to get suspicious that Colleen might be cheating. How is it possible for Colleen to always pick the best cards?

Answer:

Since Colleen knows everyone's public key (as do all the other players), it is trivial for her to compute E_KUC [E_KUB [E_KUA [m]]]] for each possible m, since there are only 52 possible m's and she knows they are 1, 2, ..., 52. She can then match the results with the deck, and know which card is which.

In general, it is not wise to encrypt guessable messages with a public key, since all an attacker has to do is try the possible messages and see if one matches.

b. (10) Suggest a simple modification to the protocol that makes it (nearly) impossible for Colleen (or anyone else) to cheat.

The easiest solution (which no one got) is for each player to just add a different random string to each card when they encrypt. So, the deck will be: E_KUC [E_KUB [E_KUA [m + R_{A, i}] + R_{B, j}] + R_{C, k}]. Since each player gets to add a random string, no player can determine the cards by trying a small number of messages. At the end of the game, the private keys are revealed, and each player can compare the random strings to make sure no one tampered with the cards.

c. (10 + up to 15 bonus points) In most poker games, cards are revealed one at a time followed by rounds of betting. Consider a poker game (5 card stud) that works as follows:

1. Dealer shuffles the deck. The dealer is one of the players, and isn't trusted. The other players can observe that the dealer shuffles fairly.
2. The player to the right of the dealer cuts the deck, just to make sure the shuffle was fair.
3. The dealer gives each player (including herself) one card face down in turn, starting with the player to her left. Each player can read her own card, but this card will not be revealed to the other players until the end of the hand.
4. The dealer gives each player (including herself) a second card, face up. All players can see the face up cards.
5. The players make bets or fold. (You don't need to worry about this part of the poker protocol.)
6. The dealer gives each player (including herself) a third card, face up.
7. The players make bets or fold.
8. The dealer gives each player (including herself) a fourth card, face up.
9. The players make bets or fold.
10. The dealer gives each player (including herself) a fifth card, face down.
11. The players make bets or fold.
12. All players still in the game reveal their face down cards, and the best hand wins the pot.

Design a protocol that supports a distributed poker game over the Internet. The closer you can get to the physical poker game described above, the better.

For bonus credit, your protocol must not allow any player to cheat, must not require a trusted third party, and should not require losing players to reveal their hands (or the dealer to reveal the unused cards) to catch cheaters. Regular credit (10 points) will be given to solutions which satisfy the no cheating requirement but not the other two. That is, if you can't solve it without a trusted third party dealer, submit a solution that uses one.

Answer:

With a trusted third party, its easy:

1. All the players generate public-private key pairs: KU_Pi, KR_Pi. The trusted third party generates a public-private key pair: KU_D, KR_D. The public keys are published. Assuming the trusted third party is trustworthy, and none of the private keys are compromised, the protocol is secure.
2. The trusted third party generates a deck of cards (using the solution from B) and shuffles them. There is no point in cutting the deck or making a player the dealer - either you trust the third party or you don't, and if you don't you shouldn't play! It is a bad idea to complicate the protocool with steps that are not necessary for security. Giving one player a chance to cut the deck is opening up your protocol to additional vulnerabilities.
3. For face down cards, the trusted third party sends each player their card as E_KRD [E_KUPi [m]. Because it is encrypted using the player's public key, no other player can decrypt the card. Because it is encrypted using the trusted third party's private key, the player can authenticate it came from the trusted third party, and can decrypt the card using KU_D.
4. For face up cards, the trusted third party sends every player E_KRD [player i: m]. Players can authenticate the message using KU_D.
5. At the end of the hand, the trusted third party reveals cards as necessary.

Without a trusted third party, its extremely difficult. The main challenge is revealing the face-down cards to one player and face-up cards to all the players without revealing anything that can be used to determine the other cards. No completely satisfactory answers were submitted.

I believe the following protocol works --- but its complicated enough, that I'm not extremely confident. If you can find a significant flaw in this protocol, that is worth 20 bonus points.

First, we introduce this protocol which can be used to produce a random value which no part may influence:

Random choice protocol

1. Alice generates random bitstring RA, publishes h (RA).
2. Bob generates random bitstring RB, publishes h (RB).
3. Colleen generates random bitstring RC, publishes h (RC).
4. After all hashes revealed, A, B and C reveal RA, RB and RC.
5. The random bitstring is R = RA XOR RB XOR RC.

Assuming h is a one-way hash function, no one can cheat, since the hashes were already revealed. Each player has to choose their contribution to the random string without knowing the other values that will be XOR'd with it.

Now, let's play poker:

1. Pick a random R using the random choice protocol. (This isn't absolutely necessary, but it makes off-line attacks difficult, since the cards will be different each hand.)
2. Alice generates a deck where each card is cardno XOR R.
3. Alice picks a secret random bitstring R_A. Each card is XOR'd with R_A. Alice sends the cards in random order to Bob.
4. Bob picks a secret random bitstring R_B. Each card is XOR'd with R_B. Bob sends the cards in random order to Colleen.
5. Colleen picks a secret random bitstring R_C. Each card is XOR'd with R_C. Colleen publishes all the cards in random order, for all players to see. The cards are now:

   Card_i = m_j XOR R XOR R_A XOR R_B XOR R_C

   No player can know which card each is because of the secret XORs and scramblings.
6. Alice generates 52 secret random bitstrings, R_Ai. Alice scambles the deck, and replaces each card with a tuple:

   Card_i = < Card_j XOR R_A XOR R_Ai, E_KUA [R_AXi]>

   Where R_AXi is a different random string for each card. Alice keeps a table mapping R_AXi to R_Ai, so when she is given R_AXi she knows the corresponding R_Ai.

   Note that the XOR with R_A removes Alice's original random string from the cards without revealing R_A to any other player.

   Alice sends the new deck, in random order, to Bob.

7. Bob follows the same protocol - scrambles the deck, XORing out R_B from each card, XORing in a new different random string for each card, for the left element of the card tuple. Bob replaces the right element of the card tuple with:

   E_KUB [old right tuple + R_BXi]

   Hence, Bob will be able to undo this encryption using his private key to get R_BXi and the Alice's right tuple (which has no meaning to Bob). Also, note that even if Alice eavsdropps on the deck Bob sends to Colleen, she cannot determine the shuffle since the left halfs have been XOR'ed randomly, and the right halfs have been encrypted with Bob's public key.

8. Colleen does the same thing as Bob. At this point, we have cancelled out R_A, R_B and R_C. Each card is encoded as:

   Card_i =
          < m_j XOR R XOR R_AiA XOR R_BiB XOR R_CiC,
            E_KUC [E_KUB [E_KUA [R_AXiA] + R_BXiB] + R_CXiC]

   The whole deck can be published.
9. Deal each player a face-down card. (Alice gets Card₁, Bob gets Card₂, Colleen gets Card₃.)
10. Alice decrypts her face-down card by sending the right half of the card to Colleen. Colleen uses KR_C to undo the outer encryption on the right half of the card and get R_CXiC. She uses this to lookup R_CiC, and sends this to Alice as E_KUA [E_KRC [R_CXiC]].

    Colleen sends Bob the rest of the right half of the card: E_KUB [E_KUA [R_AXiA] + R_BXiB.

    Bob undoes the KU_B encryption using KR_B, and obtains R_BXiB. He looks up the corresponding R_Bi and sends this to Alice encrypted with her public key and his private key. Bob also sends Alice E_KUA [R_AXiA], which she can decrypt using her public key and use to lookup R_AiA.

    Alice can now calculate m_j = (Left half of card) XOR R XOR R_CiC XOR R_BiB XOR R_AiA.

    She can view her face-down card, but no one else has obtained any information about this card of any other card.

11. Bob decrypts his face-down card similarly. The difference is he sends E_KUA [R_AXiA] and Alice sends back R_AiA, appropriately encrypted. Colleen decrypts her face-down card similarly.
12. For a face-up card, they can follow the same protocol, except each player sends their corresponding R_pip to all other players, so that every player can view the card.
13. At the end of the hand, the face-down cards for the winning player are revealed by each player revealing the corresponding R_pip. Players can detect cheating by comparing the resulting values with the deck after step 8.

This protocol is believed to be correct, but a bit unwieldy for a practical poker game! If anyone can come up with a correct protocol that requires substantially less work (it must not require a separate key for each card), that is worth 100 bonus points.

4. Hash House Harriers

(10) Lem E. Tweakit thinks he can improve on the Data Authentication Algorithm (described in Stalling, p. 252-3) when a smaller MAC is required by using Output Feedback Mode instead of the Cipher Block Chaining mode used by Data Authentication Algorithm. He produces a 16-bit MAC by using DES in 16-bit OFB mode starting with an intialization vector of zero, and uses the last ciphertext output as the MAC. Assuming 16 bits provides sufficient security for Lem's purposes, does this satisfy the required properties of a MAC function?

Answer:

The last 16-bits produced by OFB depend only on the last 16-bits of the message! Hence, an attacker can change the first n - 16 bits of the message to anything she wants without getting caught. Compare this to Cipher Block Chaining, where the last 16-bits produced do depend on the whole message.

5. Interplanetary IOUs

Consider the IOU request protocol from Lecture 9: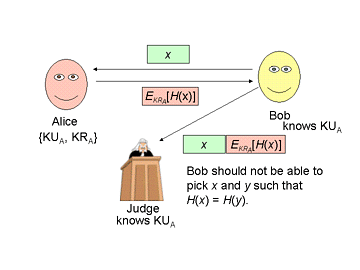 It works as follows:

1. Bob sends Alice an IOU message, x.
2. Alice computes H(x) using a cryptographic hash function, and sends Bob the hash result encrypted with her private key: E_KRA [H (x)].
3. Bob can decrypt E_KRA [H (x)] using Alice's public key to verify that Alice signed the IOU message x.
4. Bob can send M and E_KRA [H (x)] to a Judge to prove that Alice agreed to the IOU message x.

This protocol is vulnerable to the Birthday Attack since Bob gets to select x. One solution is to use a large message digest (that is, have H(x) be 128 bits). Alice is on Mars, however, and her Interplanetary Internet connection is too slow to send 128 bits reliably.

Colleen Hacker suggests that Alice only agree to sign hashes for messages of the form I, Alice, owe Bob n dollars where n is an integer (written without spaces or commas). Alice and Bob securely inform the Judge that only messages of that form should be considered valid IOUs.

a. (15) Assuming Alice will only sign hashes for messages of the given form where n is in the range 1...2¹², how much work is it for Bob to cheat? That is, how much work must he do to with high probability find a pair of messages x = I, Alice, owe Bob n dollars and y = I, Alice, owe Bob m dollars where n is agreeable to Alice (in the range 1 - 4096, there are 2¹² possible x messages) and m > 10000?

To keep the math simple, you may assume that none of the choosen x message hash to the same value as any other x message, and none of y messages hash to the same value as any other y message. Note that this underestimates the actual amount of work required.

Answer:

Using the no duplicates assumption, there are 2¹² different hash values corresponding to messages Alice will agree to sign. Bob needs find a message favorable to Bob (but disagreeable to Alice) that matches one of those has values. There are 2⁶⁴ possible hash values, so for one bad message, Bob has a 2^-64 chance of matching a particular hash value, and a 2^-64 * 2¹² = 2⁵² chance of matching one of the good hash values. If Bob generates approximately 2⁵² favorable messages, he has a good chance (but not a certainty) of finding a match. (Because of the simplifying assumptions, this was sufficient to get full credit.)

If we drop the simplifying assumption, the math gets much more complicated. Note that we cannot use the Birthday attack formula, since the number of possible good messages is limited to 2¹². We need to estimate the chances of finding a collision given different numbers of good and bad messages.

Since 2¹² is so small relative to the 2⁶⁴ possible hash values, let's assume there are still approximately 2¹² different good hash values. For each bad message we choose, we have a 2^-52 chance of matching one of those hash values. Or, there is a 1 - 2^-52 probability we don't find a match. So, if we try n bad messages, there is a (1 - 2^-52)ⁿ probability there are no matches. Or, a 1 - (1 - 2^-52)ⁿ probability of finding at least one match. We are looking for n such that this value is close to 1. Actually calculating n would require a good calculator.

b. (15) Suppose Alice owes Bob a legitimate debt of $1000, and signs a hash for the corresponding IOU message: I, Alice, owe Bob 1000 dollars. Alice refuses to pay, and Bob brings the case to Martian small claims court. He shows the Judge the IOU message and corresponding hash digest signed with Alice's private key.

Alice claims, "Yes, it is signed with my private key, but I didn't sign the IOU. A cracker broke into my machine and stole my private key, and posted it on the Internet. Bob forged the IOU. You should put Bob in jail instead of making me pay the IOU." To back up her statement, she shows the Judge a public Internet site that reveals her private key.

Suggest a way to prevent this. (Consider non-cryptographic solutions; if you find a purely cryptographic one you've done something amazing.)

Answer:

The challenge is to either make it impossible for Alice to reveal hey private key intentionally or to make it so painful she would not do so. Lots of interesting answers were submitted, but no one (in this class or the world) has come up with a totally satisfactory solution.

One approach is to use the analogy of a public notary. When someone signs an important legal document, they use human witnesses who validate their identity (using a trustworthy photo ID), watch them sign the document, and then stamp the document with a notary seal. The virtual equivalent is a trusted third party that confirms Alice's identity, and then signs the document using its private key. The problem the trusted notary can't use Alice's private key to confirm her identity, since if that key is stolen the cracker could do this also. We can use physical means to authenticate Alice to the trusted notary, but this might be difficult or expensive if she is on Mars. We can use a different key, or a combination of the key a hardware challenge/response card, but Alice could still claim this were stolen.

Many suggests adding timestamps to the IOU. This is certainly a good idea, but does not completely solve the problem. If Alice's key is actually stolen, she probably will not find out until later (perhaps, when she first sees the bogus IOU), and there is no way to tell whether her key was really stolen before or after the IOU was timestamped.

Other approaches are to make it harder for Alice to (either accidentally or intentionally) reveal her private key. We could put the key on a smart card and have a special, tamper-proof device that uses the card to sign an IOU. This can be integrated with a password and biometric (although we saw how well biometrics work in "Sneakers") so that someone stealing the card alone cannot forge IOUs.

Another approach is to deter Alice from revealing her key, by encrypting some embarrassing information with it that will also be revealed. This has two challenges - someone needs to know Alice's key and the embarrassing information to ensure that the information she encrypts with her key is really embarrassing, and will be sufficient to prevent her from deliberately revealing her private key. This requires a very trustworthy trusted party indeed!

University of Virginia Department of Computer Science CS 551: Security and Privacy on the Internet

David Evans evans@virginia.edu