Averages
Problem Set 1: Problem Set 2: 1 14/15 1 30.2/30+10 2 9.7/10 2 17.8/25 3 14.9/20+20 3 13.8/15 4 15.8/15+15 4 21.7/30 5 12.3/15+20 6 18.9/25 Total: 88/100 Total: 85/100
1. Faro Shuffling
Magicians and card sharks can perform Faro shuffles (named after a card game in which these shuffles were particularly effective for dishonest dealers) that split the deck into halves, and then perfectly interleaves the two halves. There are two forms of Faro shuffles - the out shuffle, in which the first card is taken from the top half of the deck; and the in shuffle, in which the first card is taken from the bottom half of the deck. If the deck has an odd number of cards (2n - 1), for the out shuffle the top half is split to n cards and the bottom half is split with n - 1 cards. For the in shuffle, the top half would use n - 1 cards, and the bottom half n cards.
For example, for a deck with 9 cards 0 1 2 3 4 5 6 7 8, a Faro out shuffle would split the deck into top stack 0 1 2 3 4 and bottom stack 5 6 7 8 and produce 0 5 1 6 2 7 3 8 4. An in shuffle would split the deck as 0 1 2 3 and 4 5 6 7 8 and produce 4 0 5 1 6 2 7 3 8. We could describe the 9-card Faro in shuffle as a permutation of the card positions: (0 1) (1 3) (2 5) (3 7) (4 0) (5 2) (6 4) (7 6) (8 8).
a. (10) What is the order of the Faro in shuffle on a 9-card deck? (That is, what is the fewest number of shuffles before each card returns to its original position.) (A full credit answer should show how you determined this doing something smarter than manually tracing through every shuffle.)
We can also consider Faro shuffles as a function on positions, where p is the card's position starting from 0 = top of deck and N is the number of cards:
O(p) = 2p mod N out shuffle
I(p) = 2p + 1 mod N in shuffle
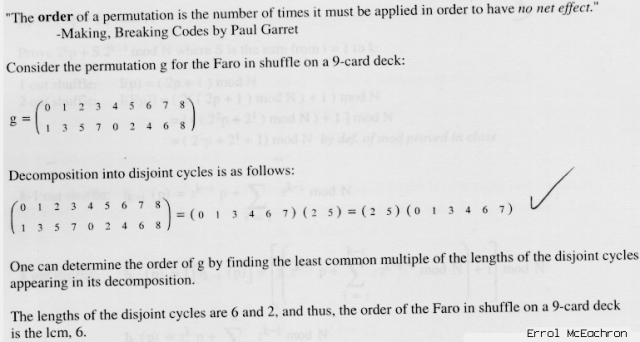
b. (5) Prove that the position of a card starting at p
after a sequence of k out shuffles is 2k p
mod N.
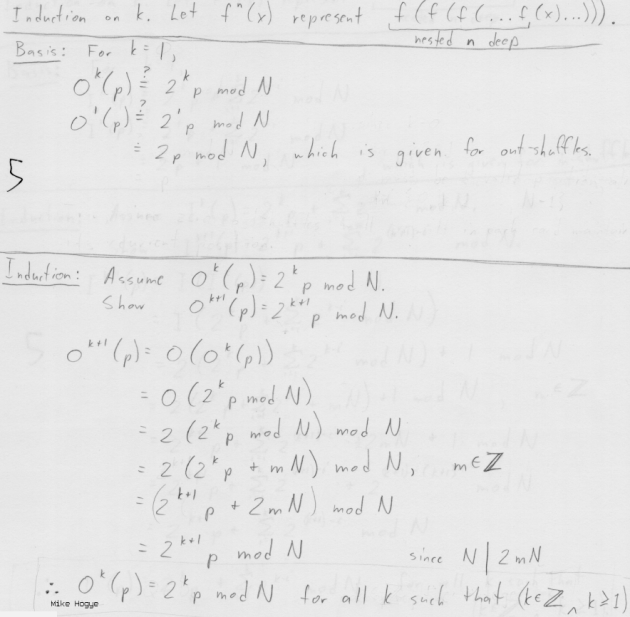
c. (5) Prove that the position of a card starting at p after a sequence of k in shuffles is 2kp + Σ 2k - i mod N where Σ is the sum from i = 1 to k.
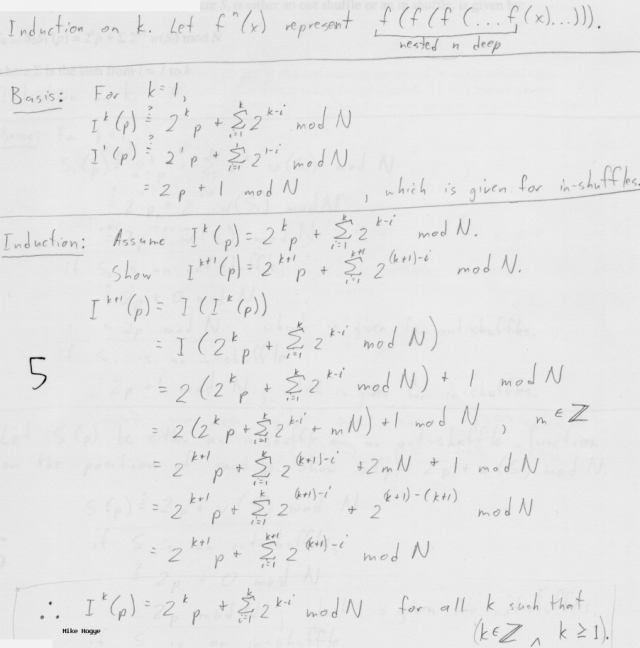
d. (5) Define w(S) = 0 for out shuffles and w(S) = 1 for in shuffles. Prove that the possition of card p after a sequence of k shuffles, Si where Si is either an out shuffle or an in shuffle, is given by:
Sk ... S2S1 (p) = 2kp + Σ 2k-i w(Si) mod Nwhere Σ is the sum from i = 1 to k.
Answer: See Stephen Liang's below.
e. (5) Cathy Sharky, noted card shark, is playing poker using a standard deck with 1 joker (53 total cards). Cathy puts the Ace on top of the deck when she picks up the cards. There are 4 other players in the game, so she wants the Ace to end up as the 5th card from the top of the deck so she deals it to herself.
Assuming Cathy is adept at performing perfect in and out shuffles (as would be any qualified card shark), how should she shuffle the deck? (Since we number the positions 0..52, this means we are looking for a sequence of permutations such that P(0) = 4 where P = some sequence of I and O shuffles.)


f. (up to 10 bonus points) Devise a general way Cathy can determine a sequence of in and out shuffles that will move the top card on the deck to an arbitrary position in the deck? (Hint: You may assume that before embarking on her career as a card shark, Cathy took some CS courses and is well adept at converting between decimal and binary.)

2. Enigma
The cryptanalysists at Beltchley Park (no relation to Bletchley Park), have recovered a mechanical cipher device used by their arch-enemies the Jansonites. The device appears to be a variant on the Enigma machine. It consists of two rotors and a reflector:
________ ________ _______
| | | | | |
Plaintext ------>| |--->| |--->| |
| | | | | |
| L | | M | | R |
| | | | | |
Ciphertext <-----| |<---| |<---| |
|______| |______| |_____|
Rotor 1 Rotor 2 Reflector
Both rotors contain the alphabet in order. Hence, in position 1, the rotor maps A -> A, B -> B ..., Z -> Z. In position 2, the rotor maps A -> B, B -> C, ..., Z -> A. Rotor 1 advances one position for every letter. Rotor 1 has a ring, that make Rotor 2 advance once. Hence, Rotor 2 will advance one position every 26 letters. The ring is always set so that Rotor 2 will advance after the 26th letter (and every 26 letters after that). In the reverse directions, the rotors have the inverse mapping (e.g., in position 2, rotor 1 in the reverse direction maps B -> A.)
The reflector connects A <-> N, B <-> O, C <-> P, ..., M <-> Z.
a. (5) Charles Blabbage claims that decoding messages encoded with the Jansonite Enigma machine is as hard than breaking the Vigenere, which they are convinced is indecipherable (of course, we know better). Show that breaking the Jansonite Enigma cipher is no harder than breaking a Vigenere cipher with a key or a particular length.
Answer: There are at least three reasonable ways of thinking about this:
- The Jansonite Enigma is not harder to break than a Vigenere with a 262 length key, since the Enigma is producing ciphertext, ci = Li(Mi (R (αi))) and Li (rotor 1 after i steps) is k1 + i mod 26 where k1 is the initial position or rotor 1. Similarly, Mi = k2 + (i div 26) mod 26. This is like a Vigenere with key length 262, since after 262 letters Rotor 1 and Rotor 2 will both be in their original position.
- The keyspace for the Jansonite Enigma is 262 (there are only two letters to choose for the key orientations). For a brute force search, this is equivalent to a 2-letter Vigenere key.
- The Jansonite Enigma is equivalent to a Vigenere with the 1-letter key "M". The rotors always cancel themselves out on the return path. The reflector adds 13 mod 26.
b. (5) Although Blabbage showed the Jansonite Enigma cipher is no harder to break than the Vigenere cipher, this does not mean it is not easier to break. Describe a more effective attack.
Answer: Mi = Ci + 13 mod 26. The effect of the Jansonite Enigma does not depend on the key at all!
c. (15 + possible bonus) The Jansonites believe a more confusing reflector is the key to improving their cipher. They replace the reflector with a random letter mapping, unknown to Beltchly Park. Note that unlike the real Enigma reflector, their reflector is not an involution. It can be any monoalphabetic substitution. It is known, however, that all messages on a particular day are encrypted with the same day key, and start with the message key repeated three times. The message key is two letters giving the initial rotor orientations for Rotor 1 and Rotor 2. Since the Jansonites are extremely lazy, it is known that the message key is always two identical letters. Hence, you can assume that the first six letters transmitted are all identical (e.g., "FFFFFF" or "UUUUUU"). On one day Beltchly Park intercepted the following ten encrypted messages:
Each of there messages corresponds to six identical letters encrypted starting with the same rotor orientations.DJOXYM GVLCAS UYTQLH OAHFZF CQQEHB BIGAGL PLWLXE EWSWRO VSNJUJ FDVRVQ
Determine everything you can about the reflector and day key. (You will receive some credit for determining anything useful about the reflector or day key. For full credit, you must determine a possible reflector and day key setting. For bonus points, you must determine everything that can be determined from the available information and argue convincingly why it is not possible to determine nore.)
Answer:The key insight is that you can cancel out the effect of the rotors by advancing the ciphertext letters.
Ci = Li-1 (Mi-1 (R (Mi (Li (α)))))
Since Rotor 2 is known to not turn, we can combine the effects of the two rotors into Pi (α) = k1 + i + k2 + α mod 26 = k + i + α mod 26.
Hence:
Ci = Pi-1 (R (Pi (α)))
Ci = R (α + k + i) - k - i
We know the six plaintext letters are the same for each message, so:
C0 = R (α + k) - k
C1 = R (α + k + 1) - k - 1
C2 = R (α + k + 2) - k - 2
...
C5 = R (α + k + 5) - k - 5
We can more the -i to the other side of the equation. For example, for the first message we have: DJOXYM. So:
D = R (α + k) - kSuppose we guess k = 0, then we know R(α) = D, R(α + 1) = K, ... R(α + 5) = R.
J = R (α + k + 1) - k - 1 ==> K = R (α + k + 1) - k
O = R (α + k + 2) - k - 1 ==> Q = R (α + k + 2) - k
X = R (α + k + 3) - k - 1 ==> A = R (α + k + 3) - k
Y = R (α + k + 4) - k - 1 ==> C = R (α + k + 4) - k
M = R (α + k + 5) - k - 1 ==> R = R (α + k + 5) - k
We can use the other messages to find other sub-sequences for R. For example, from message 5 we have CQQEHB:
C = R (β + k) - kNote the duplication of CR from message 1 letters 5 and 6 and message 5 letters 1 and 2: C = R(β + k) = R(α + k + 4). We know R must be a one-to-one function, hence β + k = α + k + 4. So, correlating the results from message 1 and message 5 give us R(α + k) ... R(α + k + 9) = [ D, K, Q, A, C, R, S, H, L, G].
Q = R (β + k + 1) - k - 1 ==> R = R (β + k + 1) - k
Q = R (β + k + 2) - k - 1 ==> S = R (β + k + 2) - k
E = R (β + k + 3) - k - 1 ==> H = R (β + k + 3) - k
H = R (β + k + 4) - k - 1 ==> L = R (β + k + 4) - k
B = R (β + k + 5) - k - 1 ==> G = R (β + k + 5) - k
Similar overlaps from the other 9 messages give us enough information to find mappings for the entire alphabet: R(α + k) ... R(α + k + 26) = [DKQACRSHLGWNFEXUZVTPMYOBJI].
Each possible guess for α and k gives us a different reflector mapping. These correspond to different initial rotor setting and messages. Note that we cannot combine those into one guess --- even if a given message can look the same coming out of M for a different rotor guess, it will not look the same as ciphertext because the effect of the return rotors after R will be different.
So, there are 262 possible reflector settings, each completely determined by our choice of the initial message letter and rotor settings. That is, given any guess for the first message letter and initial rotor configurations, we can determine the reflector settings from R(α + k) ... R(α + k + 26) = [DKQACRSHLGWNFEXUZVTPMYOBJI]. We can't tell the different between setting where the sum of Rotor 1 and Rotor 2 is equal however. So, for a given α and k guess, there are 26 possible settings for Rotor 1 + Rotor 2 = k. Hence, we know there are 263 possible initial configurations of the rotors and R.
One possible configuration is to choose α = C and k = 5. Then R = [URDTGONIPVFHWXMQLBSKJCZEAY] and the message keys are CC, LL, RR, YY, GG, ZZ, VV, PP, TT, OO.

3. Fiestel Ciphers
Ben Bitdiddle has invented a Feistel cipher and hired you to check if it is secure. His cipher opreates on 64-bit block and consists of 4 rounds. For each round: L_i = R_i-1
R_i = L_i-1 XOR F (R_i-1, K)
F (m, k) = k XOR m
The same 32-bit key, K is used for each round. The final
ciphertext is: C = R_4 || L_4.
You are given the plaintext-ciphertext pair:
plaintext: 0001100100001101011101001100011101101011010100010011101001100010 ciphertext: 0111001001011100010011101010010101101011010100010011101001100010Ben is stubbornly convinced of his genius and the invincibility of his cipher, and is not disturbed by the odd similarily between the second half of the ciphertext and the second half of the plaintext.
(15) Convince Ben the cipher is insecure by determining the key used for the plaintext-ciphertext pair shown above.
Answer: In Ben's cipher, the key XOR's itself out.Input: P = L0 || R0
Round 1:
L1 = R0
R1 = L0 XOR R0 XOR KRound 2:
L2 = R1 = L0 XOR R0 XOR K
R2 = L1 XOR R1 XOR K = L0 (the K's and R0's cancel)Round 3:
L3 = L0
R3 = L2 XOR R2 XOR K = R0Round 4:
L4 = R3 = R0
R4 = L3 XOR R3 XOR K = L0 XOR R0 XOR KC = R4 || L4 = L0 XOR R0 XOR K || R0
K = R4 XOR R0 XOR L0
R4 = 01110010010111000100111010100101 (from the ciphertext) R0 = 01101011010100010011101001100010 (from the plaintext) R4 XOR R0 = 00011001000011010111010011000111 L0 = 00011001000011010111010011000111 (front the plaintext) K = R4 XOR R0 XOR L0 = 00000000000000000000000000000000
4. DES
a. (10) Quadruple DESLem E. Tweakit doesn't think Triple DES is secure enough for encoding his secret sauce reciple. So, he adds an additional stage to Triple DES: C = Ek_4 (Ek_3 (Ek_2 (Ek_1 (P))))) where Ek_n means DES encrypt using key k_n.
He uses 4 different 56-bit keys, and believes his cipher has and effective key size of 224 bits.
Is he right? (Estimate the actual key space a brute force attack would need to search.)
Answer: No - the key space is more like 2113, since is it vulnarable to a meet-in-the-middle attack. We have C = Ek_4 (Ek_3 (Ek_2 (Ek_1 (P))))). For known plaintexts and ciphertexts, we calculate X = Ek_2 (Ek_1 (P)) = Dk_3 (Dk_4 (C)).
b. (10) DES Complement
Prove that C = DES (P, K) implies
C^ = DES (P^, K^) where M^ is the bitwise complement of
M and DES (P, K) is the output of DES encrypting P
with key K. (Hint: show (A XOR B)^ = A^ XOR B.)


c. (10) By how much does the property you proved in 4b reduce the amount of work required for a known plaintext brute force attack? What about for a ciphertext only brute force attack?
Answer:If you are doing a chosen-plaintext attack, you can obtain two plaintext-ciphertext pairs (P1, C1) and (P2, C2) where P1 = P2^. Try encrypting P1 using half of the key space (all keys whose least significant bit is zero). If you get C1 using key K, K is likely to be the real key. If you get C2^, then K^ is likely to be ther real key. Otherwise, neither K nor K^ can be the real key. You only need to run DES once to eliminte 2 keys, and bitwise complement is inexpensive, so this approximately halves the amount of work required.
For a known plaintext attack, the complement property is unlikely to help much. In fact, with enough plaintext pairs it does aid differential cryptanalysis. (See Differential Cryptanalysis of DES-like Cryptosystems, Biham and Shamir, 1991 for more details.)
If you are doing a ciphertext only attack, it is clearly useful. You can try all possible plaintext blocks with half the possible keys. If results C, you may have the correct key; if C^ results, K^ may be the correct key (and P^ the corresponding guessed plaintext).
