Block LU Factorization
LU Decomposition or Factorization is another common problem is linear algebra. In this problem, the argument matrix of a system of linear equations is decomposed into an upper and a lower triangular matrix to facilitate Gaussian Elimination. The technique is originally invented by Alan Turing 85 , and many algorithms have been developed for it due to the importance of the problem. All these algorithms progress in a diagonal fashion by adding one or more entries in the upper and lower triangular matrices in each step based on computation done on unaltered parts of the original argument matrix. For numerical stability, most algorithms permute the order of either rows or columns of the argument matrix during the decomposition process. The permutation technique is called pivoting, and the algorithms are, accordingly, classified as LU Factorization with Partial Pivoting.
All parallel implementations of LU Factorization involve heavy communications of shared data update. This is the reason we have chosen LU Factorization as our second test problem. IT implementations of LU Factorization shows that the automatic data dependency resolution demanded by IT can be realized efficiently in the back-end compilers. Furthermore, this is a problem where index reordering data partitioning is essential for computation load balancing. Therefore, the implementations expose the cost of IT ’s automatic index transformation also.
We have several IT programs implementing different LU Factorization algorithms. For the performance experiment, we only used a blocked algorithm that has an embedded SAXPY (c = αc + βa x b) operation for better temporal locality. We call the algorithm Block LU Factorization.
Multicore Block LU Performance
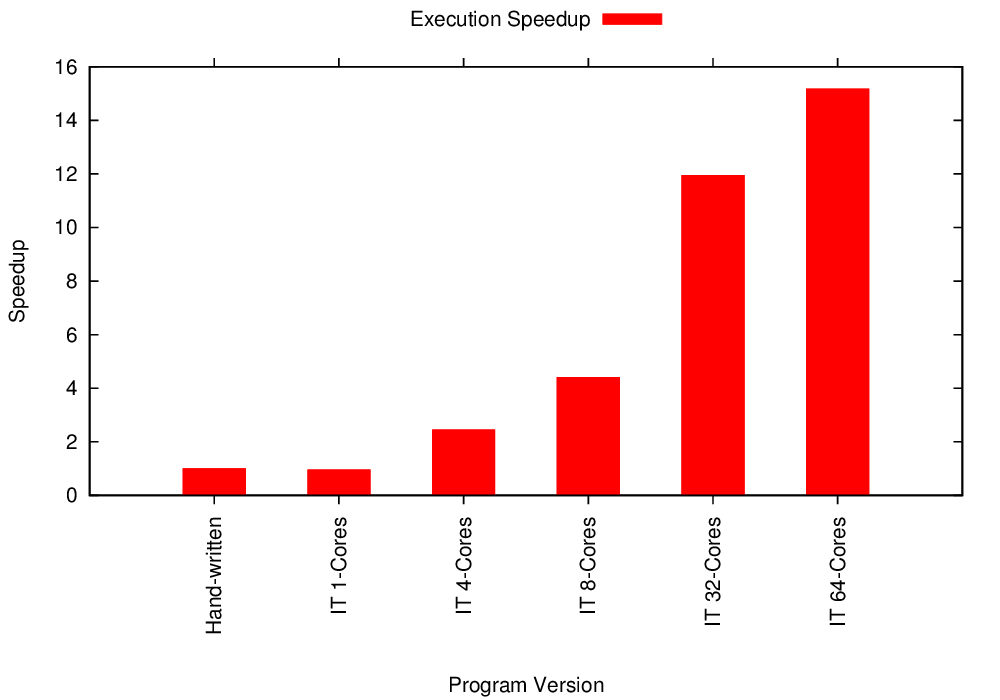
Multicore Block LU Strong Scaling
Segmented Block LU Performance
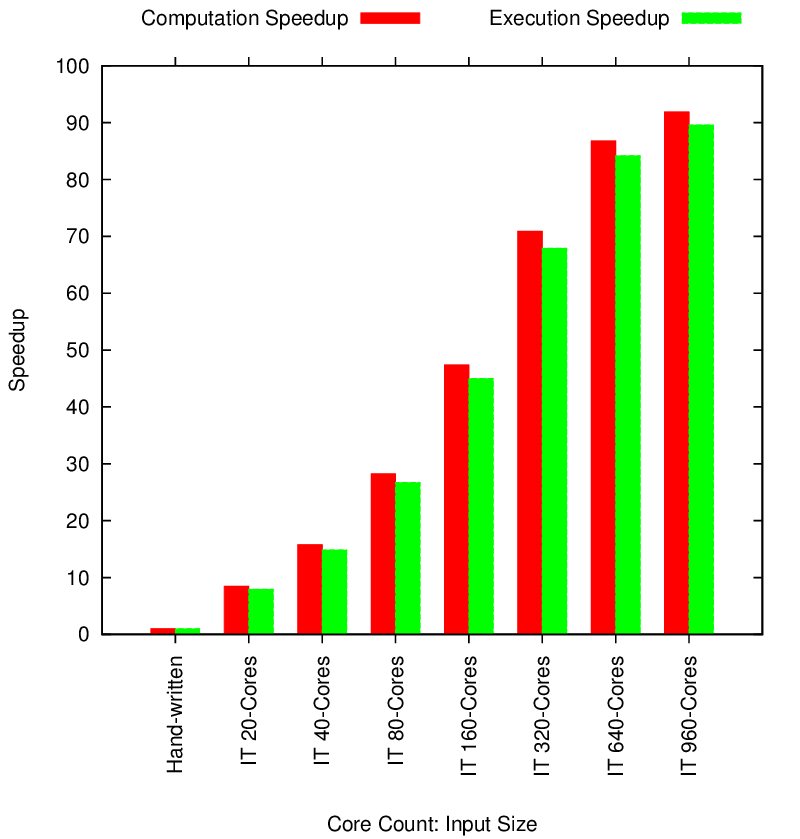
Segmented Memory Block LU Strong Scaling
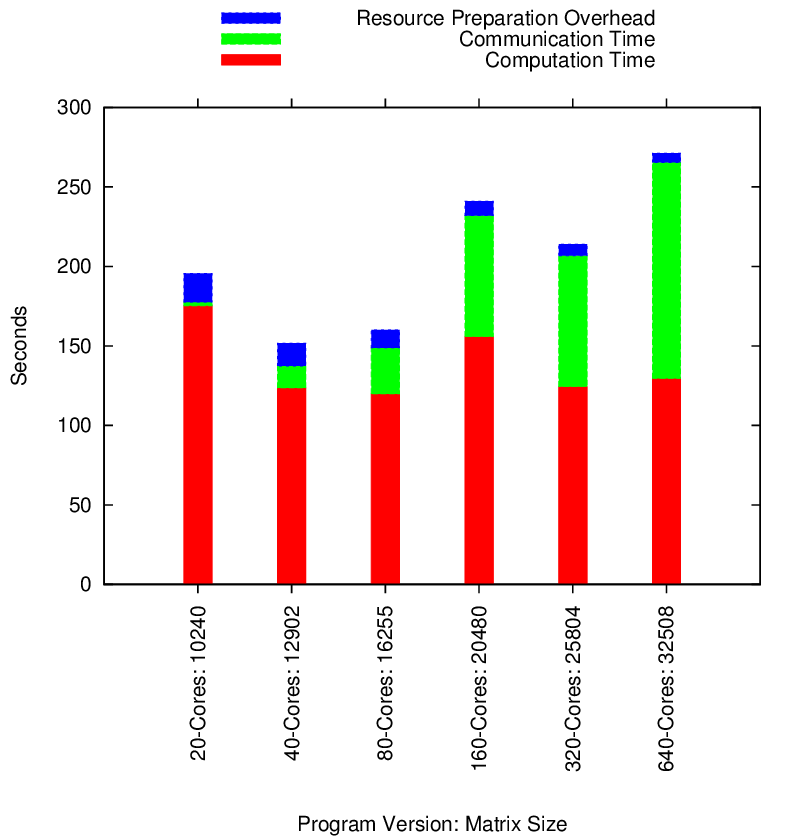
Segmented Memory Block LU Weak Scaling
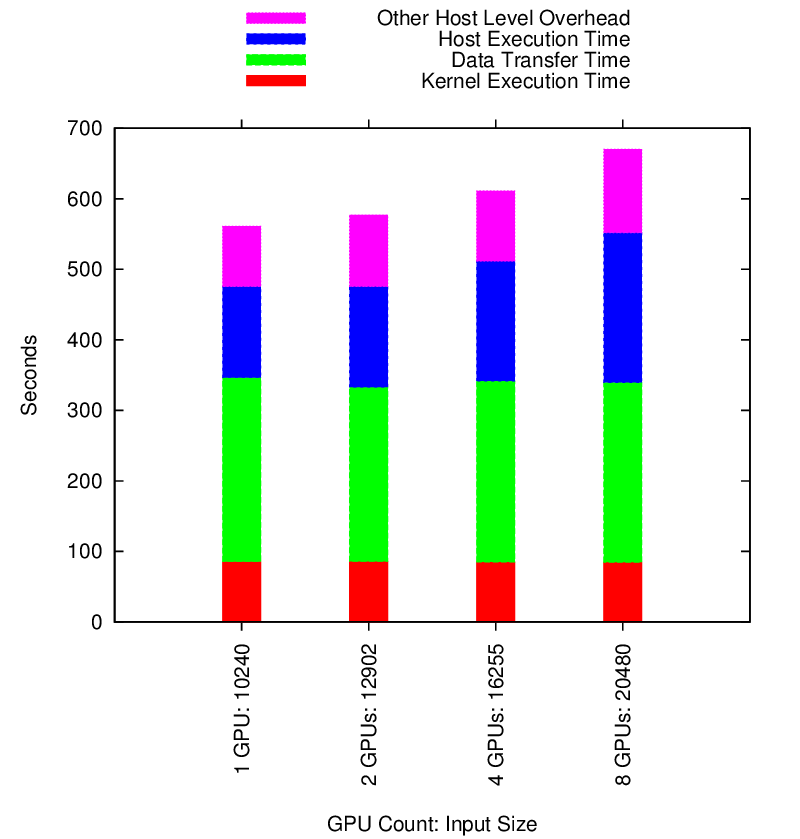
Hybrid Block LU Performance
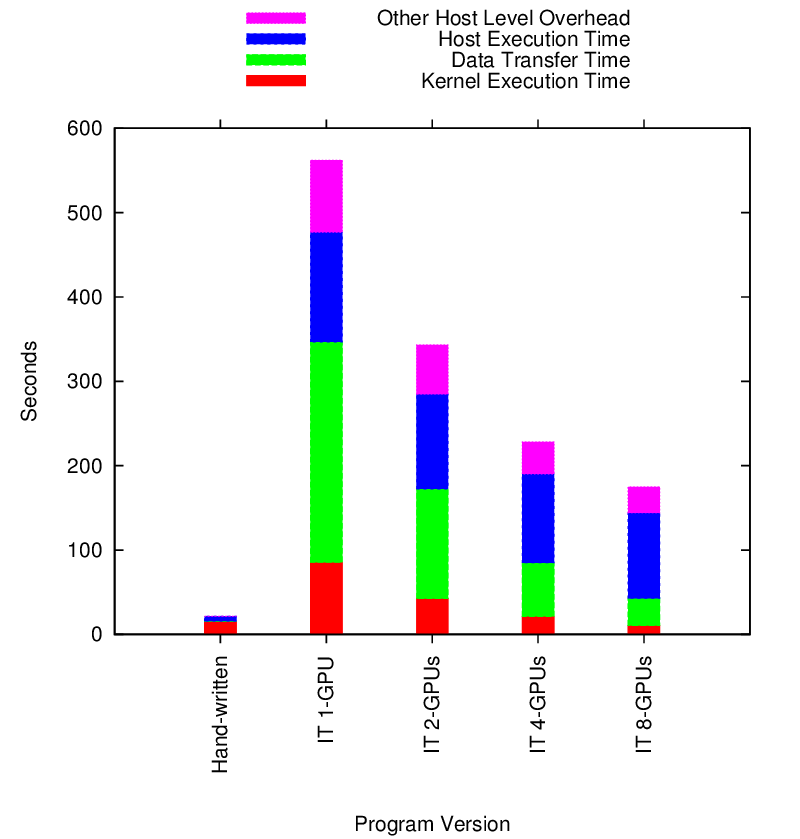
Hybrid Block LU Strong Scaling