Conjugate Gradient
Conjugate Gradient is the most prominent mechanism for solving a sparse system of linear equations. The normal strategy of Gaussian Elimination using matrix factorization is unsuitable for most sparse systems as sparse matrices in practical problems are usually several factors larger than their dense counterparts. Conse- quently, the factoring may be impossible because of limited memory or very time consuming when it is doable. Alternative algorithms for sparse matrices exploits the fact that most entries in a sparse matrix are zeros and avoid storing and computing over those entries.
Conjugate Gradient is an iterative method applicable for symmetric, positive-definite matrices. It applies a logic of steepest descent of the gradient of a quadratic form of the sparse matrix to quickly converge into the solution. We have implemented the algorithm for random sparse matrices stored in compressed row format (CSR). Although the sparse matrices of practical problems are often regular structures (e.g., a diagonal band matrix), we have decided to implement the algorithm to work on the most generic and random CSR format. This is because an algorithm on a regular, partition-able sparse matrix does not reveal anything new about the PCubeS + IT paradigm after Matrix-Matrix Multiplication and LU Factorization. In particular, we wanted to investigate the impact of irregular memory accesses on the performance of an IT program as we increase the degree of parallelism.
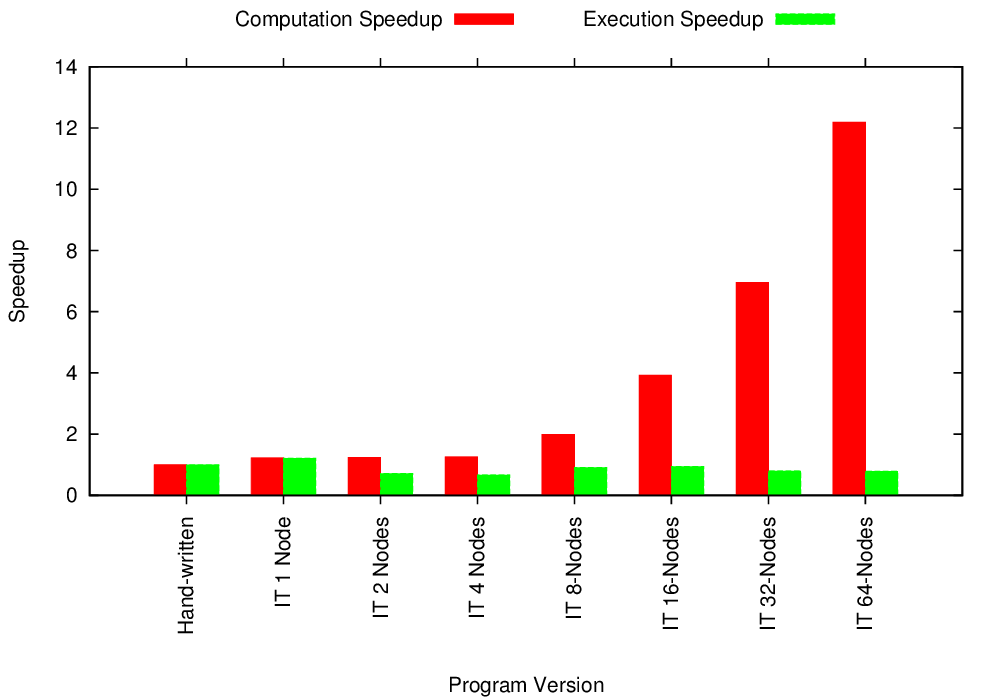
Multicore Conjugate Gradient Performance
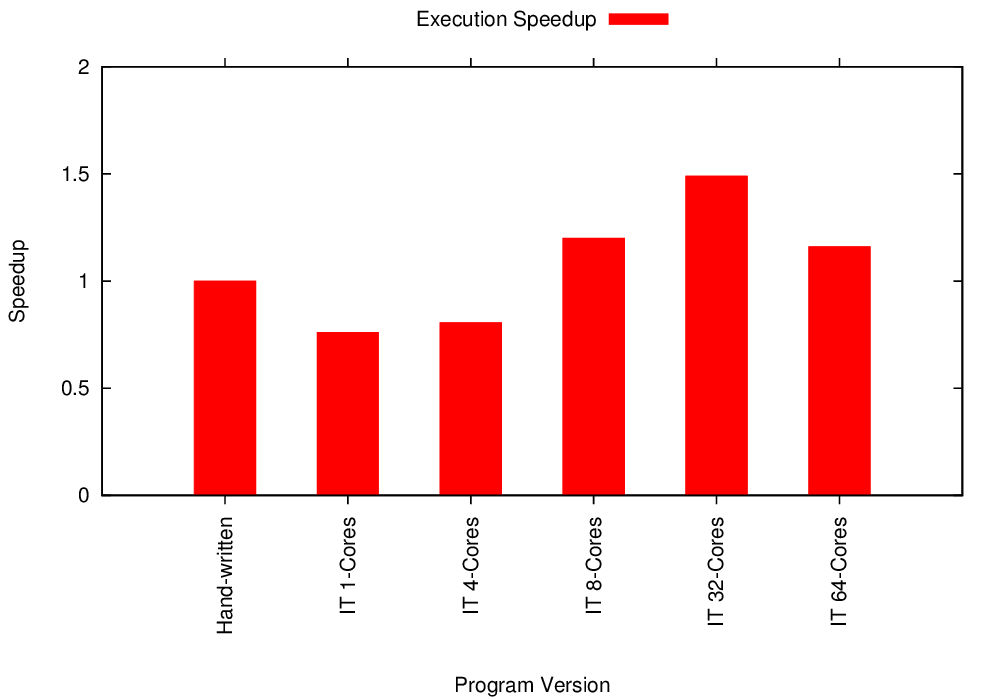
Multicore Conjugate Gradient Strong Scaling
Segmented Conjugate Gradient Performance