Five Point Stencil

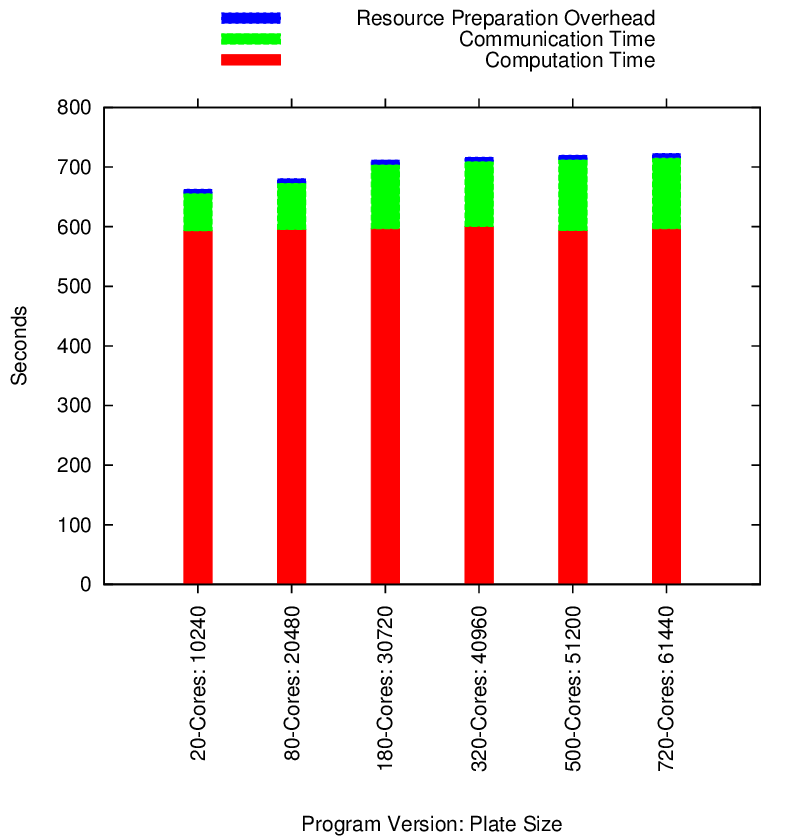
5-point iterative stencil is a numerical differentiation technique on two-dimensional grids. In this problem, the next value of a point in the grid is computed from its current value and values of its four neighbors 7 . 2D and 3D stencil problems are common in Molecular Dynamics, Image Processing, Cellular Automata and many other fields. A critical aspect of all parallel stencil algorithms is that they involve boundary sharing among neighboring data partitions and consequent exchange of updated points in the overlapped regions. This is a difficult feature to implement in a generic way – nonetheless, IT supports that. We wanted to verify the effectiveness of the feature implementation.

The algorithm we have implemented uses Jacobi iteration 7 with Dirichlet boundary condition Dir to measure heat propagation on a simulated heated plate problem. Like most stencil programs, our implementation is memory bound. Note that straightforward stencil with Jacobi iteration has the problem of slow convergence and many applications similar to our simulated problem use more advance techniques such as Adaptive Mesh Refinement and Multigrid. Supporting basic stencil is the first step toward enabling those techniques in IT.

Multicore Stencil Performance

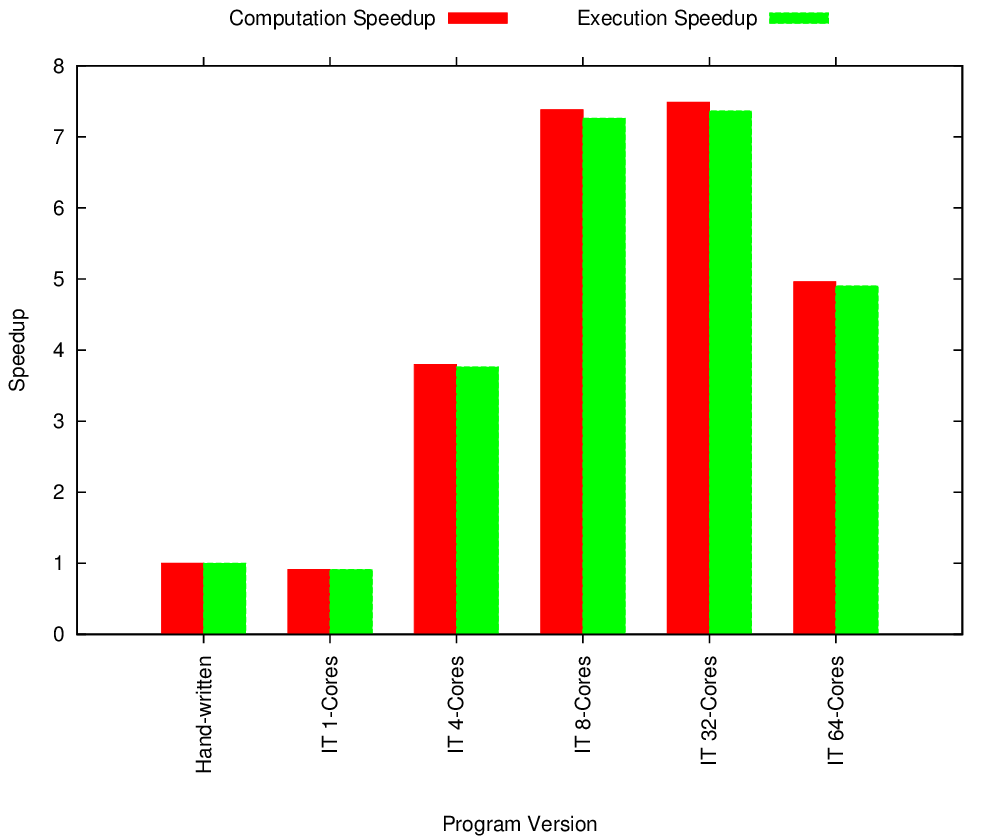
Multicore Stencil Strong Scaling

Segmented Stencil Performance

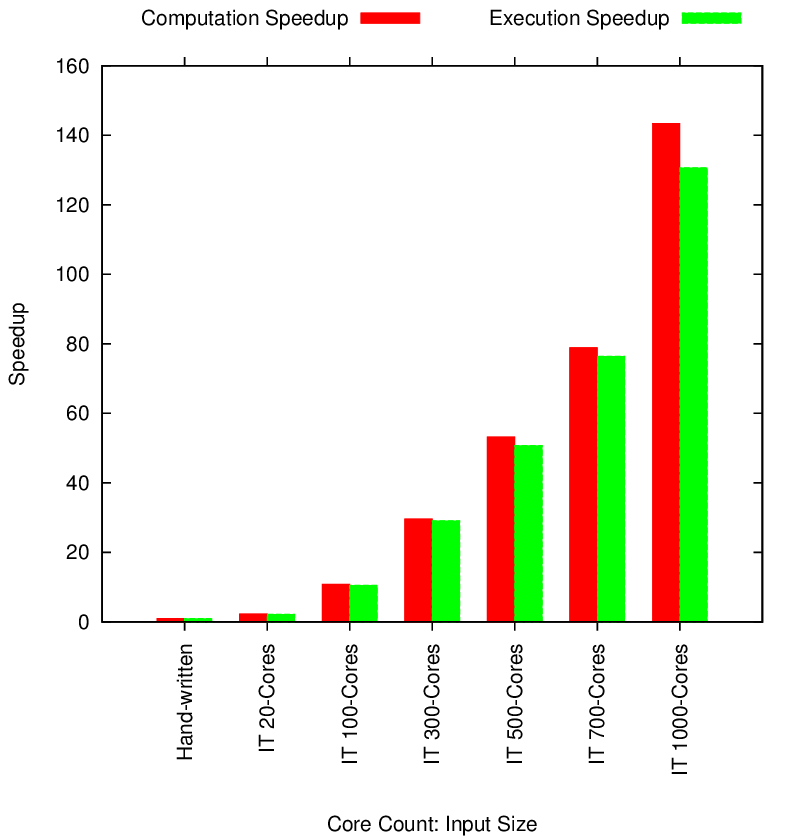
Segmented Memory Stencil Strong Scaling