Matrix Multiplication
Matrix-Matrix Multiplication is, arguably, the most important problem in linear algebra and a building block element to numerous larger applications. In this problem, a result matrix is computed by multiplying two argument matrices. Each (i, j) th entry in the result is the dot product of i th row and j th column of the first and second argument matrices respectively. The problem has O(mn 2 p) asymptotic time complexity for argument matrices of dimensions m × n and n × p. Matrix-Matrix Multiplication is a memory bound problem and its straightforward implementation suffers from severe cache misses for larger matrices. We implemented an alter- native algorithm that divides the matrices into blocks, multiplies the blocks, and then accumulates the partial results to generate the final output (check the supplementary material ‘Using Blocking to Increase Temporal Locality’ of the book 23 for the algorithm). This incremental result construction process makes the program more compute bound. We refer to the algorithm as the Block Matrix-Matrix Multiplication.
Multicore Matrix Multiply Performance
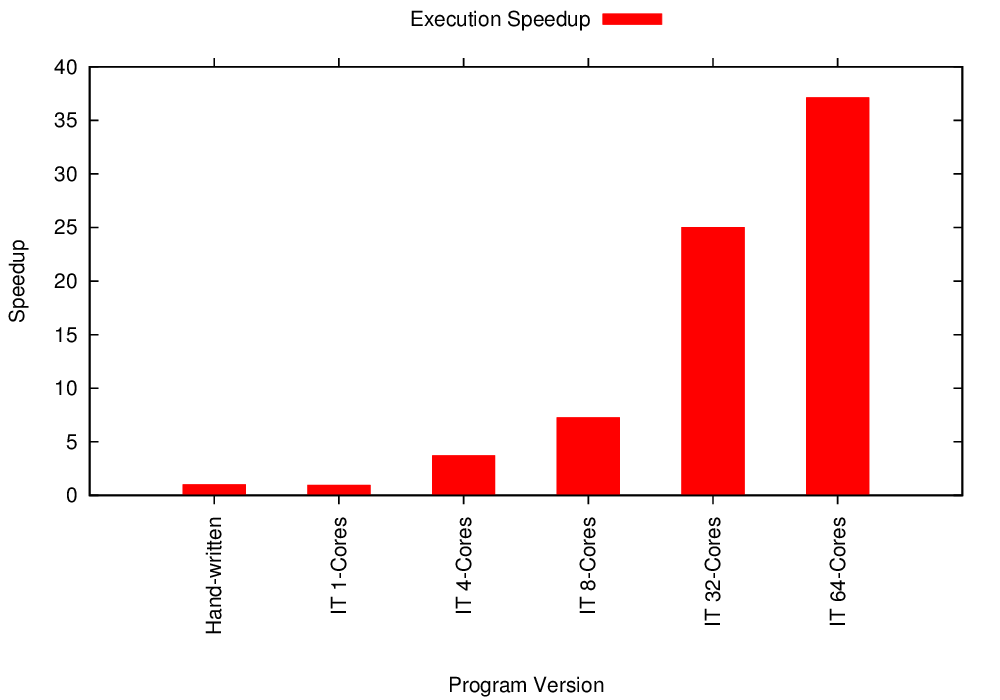
Multicore Matrix Multiply Strong Scaling
Segmented Matrix Multiply Performance
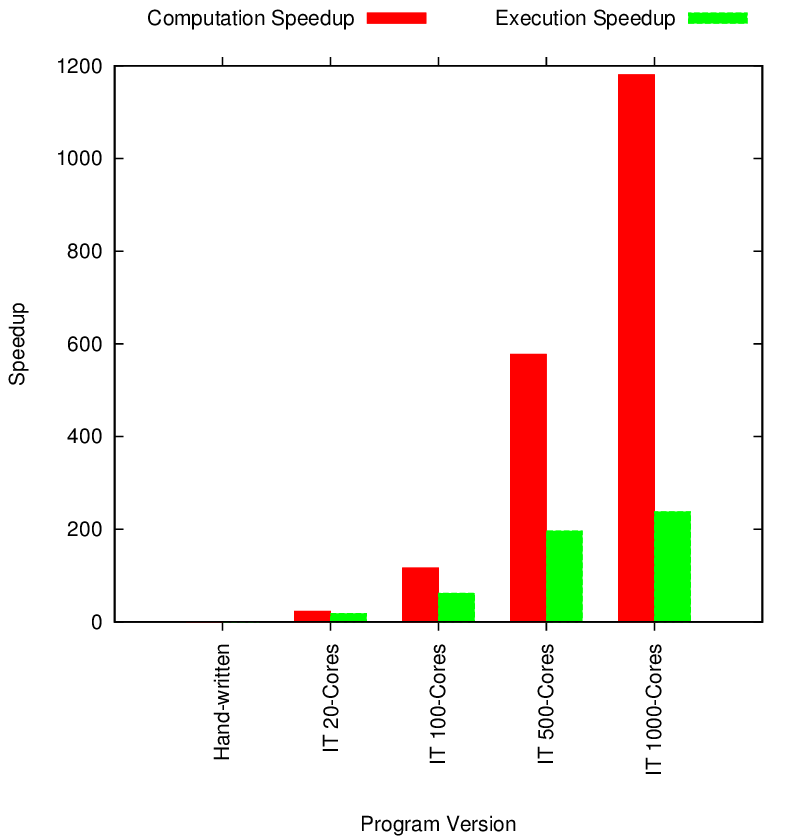
Segmented Memory Matrix Multiply Strong Scaling
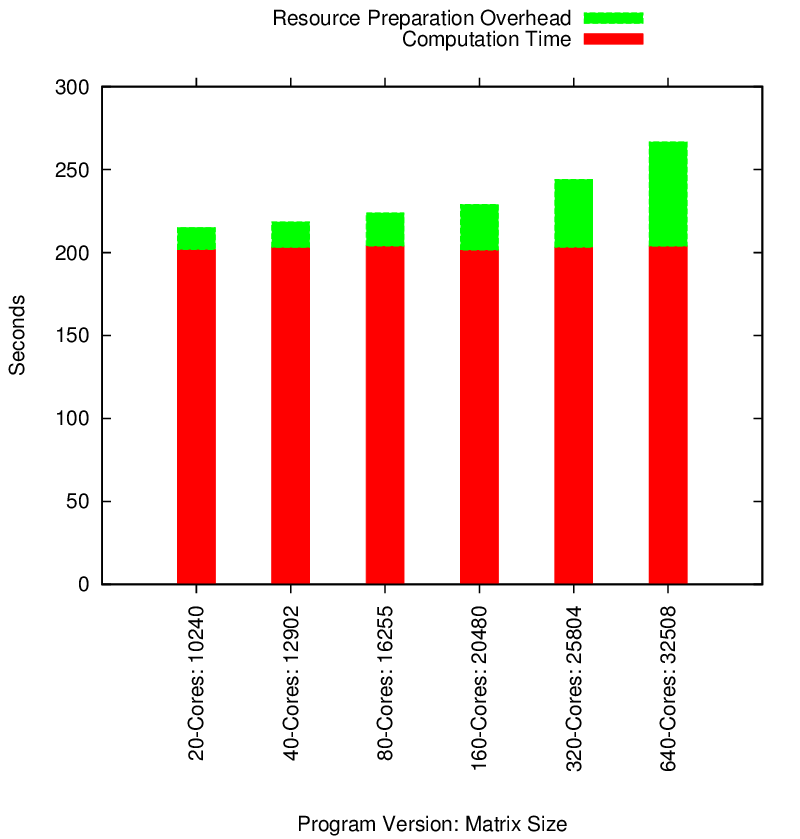
Segmented Memory Matrix Multiply Weak Scaling
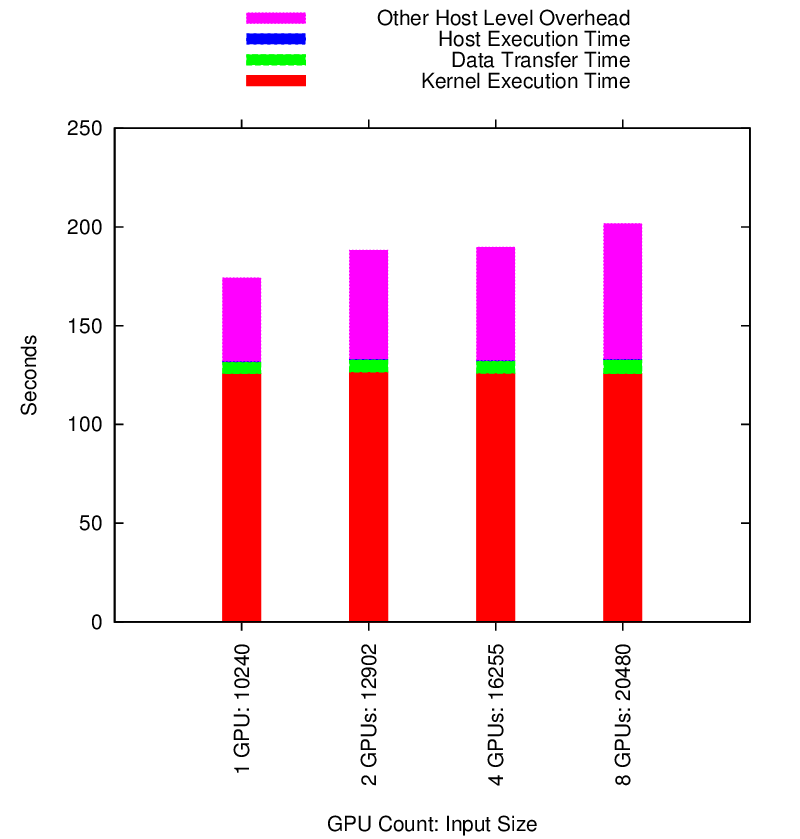
Hybrid Matrix Multiply Performance
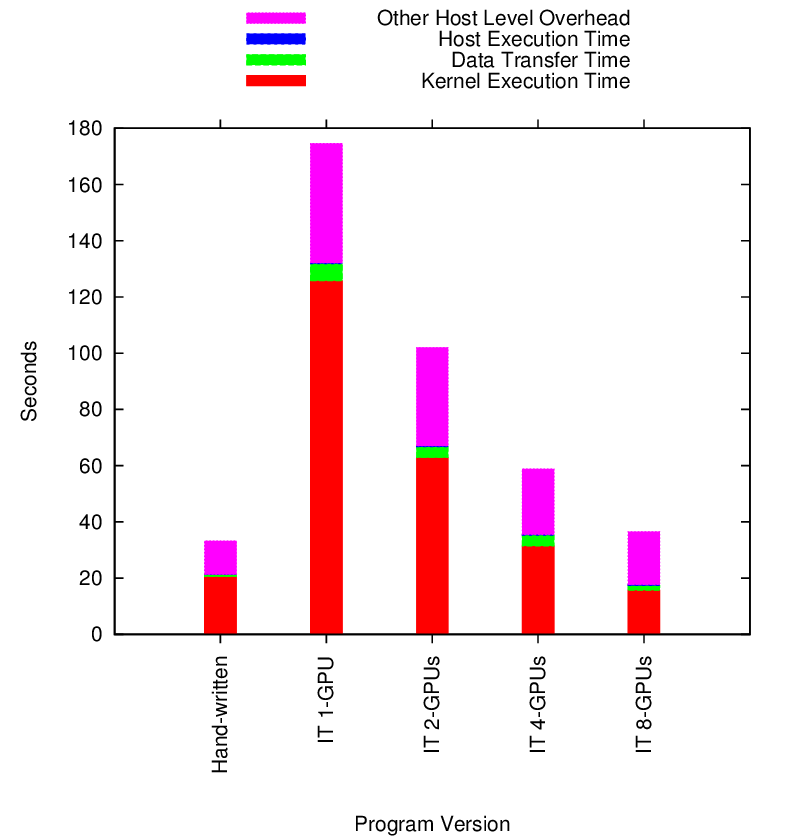
Hybrid Matrix Multiply Strong Scaling