the derivative of
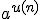 is
is 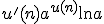
Turn in solutions to these problems:
Important: Put the answer to each question on a separate sheet of paper (or one problem on front and another on the back). This is to make grading easier for us.
Collaboration Rules for This Assignment:
Problem B1: General Problem Solving
Rotate a vector or array of n elements left by i positions. In other words, x[1]...x[i] x[i+1] ... x[n] becomes x[i+1]...x[n] x[1]...x[i]. So if i=3 then "abcdefg" becomes "defgabc". Another way of saying this is that AB become BA where A is the subsequence of the first i elements and B is the remaining elements.
The obvious solution is use a temporary scratch vector of proportional to n to build the solution, but this has space complexity BigTheta(n). Do it with just a constant number of extra variables, i.e. in BigTheta(1).
(One real-life example of this problem is cut-and-paste in a word processor. You chose a block of bytes, cut them, and then paste them somewhere else. So the block of bytes that looks like this ABCD becomes ACBD when you cut A and paste it between C and D.)
You're given a large dictionary of English words (n words). Find an efficient way to find all sets of anagrams (i.e. words that are composed of the same letters). To describe the efficiency of your solution, you may assume all words have size m (if you need to know this). If you need it, you can assume you have an efficient sort algorithm, i.e one that's BigTheta(n lg n).
You have a set of n gold coins that should have the exact same weight, but you know that exactly one of them is fake and has a different weight.You also have a balance scale, which allows you to compare two piles of coins to see which pile is lighter or if they're equal. You can assume that the fake coin is lighter than a real one.
Describe an algorithm for finding the fake coin by doing the fewest weighings. Give a formula for the number of weighings. Does your algorithm have to change if you don't know in advance whether there's a fake coin or not?
(A) We've seen an algorithm that finds the maximum element in a sequence in n-1 operations by scanning through the sequence from the 2nd to the last item, updating the current maximum if needed. But, those of you who are sports fans know that tournaments or "play-offs" find the best team (or player) by organizing "comparisons" (i.e. games) between pairs of teams, with the winner advancing to play some other winner in another round. The winner of the final round is the best (or maximum) of the original set.
Question: Assuming that the number of teams n is some power
of 2 (say 2k), show the number
of comparisons needed in such a play-off to find the best team. (Hint:
it will help if you draw out a tournament
tree and think about the math associated with binary trees.) Also, is
this optimal in the worst-case? Why or why not?
(B) If we want to find the 2nd best team (or say the 2nd largest item), then we can implement this by doing two "scans" through a list of items. The first finds the maximum, which could then be moved to the first position. The second scan skips the first item (the max) and finds the next largest. Convince yourself that you understand this approach, and that it does 2n-3 comparisons.
Question: Describe an algorithm that uses the "play-off" approach listed above that finds the second largest in fewer operations. Give the formula for the number of comparisons your algorithm uses. (The key to this approach is to reduce the number of possible candidates for the 2nd largest item. It might be that it could require more complicated processing to store and remember things, but for this question we're just trying to reduce the number of comparisons.)
Let a and b be real numbers > 1. If a < b show that an belongs to LittleOh(bn), that is an grows more slowly than bn.
Prove lg n belongs to LittleOh(nk) for any k > 0. This of course means that the log function grows more slowly than any polynomial (even those with fractional powers, e.g. 0.00001).
Prove nk belongs to LittleOh(an) for any k > 0 and a > 1. You're thus proving that all polynomials (no matter how large their degree) grow more slowly than any exponential function an when a>1.
Hint: you may need the following derivative, and you may need to use
it more than once:
the derivative of 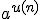 is
is 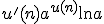
Also, you can assume that k is a whole number for this proof.
Draw the decision tree for the binary search algorithm with n=17.