
Bending spacetime, not the rubber sheet.
Sometimes in an effort to explain a concept someone comes up with a really bad image. One such is the far too common image of Einsteins’ theory of gravity, such as this version from Wikipedia:
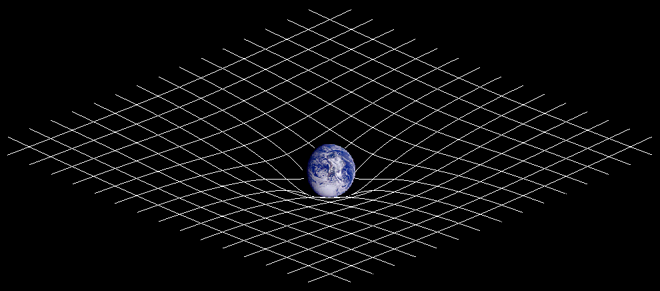
This visualization was created by some well-intentioned person, but because of it people get the impression that objects “roll down hill” toward heavy objects, which is not what’s happening at all.
The first thing to understand about Einstein’s theory of gravity is that is bends spacetime. Spacetime is a geometric representation of motion, with space on the x axis and time on the y axis. Thus this animation:

would be drawn as this spacetime:

There’s a lot that can be said about such spacetime graphs, but for now we note just two things: first, that even to stay still in a spacetime there is still a “path” a particle follows; and second, that straight paths correspond to inertial (constant-velocity) movement.
What does it mean for a path to be straight? On a flat surface this is pretty obvious, but on a curved surface it is less clear. I find the following analogy helpful.
Imagine I have a cart with two wheels side by side. If those wheels turn at the same rate (and are the same size) then the cart will move straight forward. If, on the other hand, one wheel turns faster than the other then the cart will turn towards the side with the slower wheel. With the appropriate mathematical generalizations, a two-wheeled cart with both wheels spinning at the same speed travels in what is called a geodesic, the most common meaning of “straight”.
Now imagine that there is a bump in the road under my cart’s left wheel but not under its right wheel. If we keep the wheels moving at exactly the same speed, the left wheel will use a little of its motion to roll up the bump and back down again, meaning it moves forward just a little bit less.

Because the left wheel makes less forward progress, the geodesic turns just a little bit to the left.
Einstein’s theory of gravity states that gravity causes geodesics in spacetime to curve the same way a bump under one wheel of a cart causes geodesics to curve. But since it’s spacetime, these bumps are better visualized as ripples rather than depressions in the spacetime sheet.
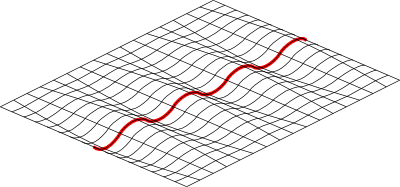
Because the ripples are larger near heavy objects, the wheel nearer a heavy object will travel up and down more than the other wheel, meaning they will make less forward progress, meaning geodesics will curve toward the gravitational source.
It is worth observing here that the ripples are moving “up” and “down”, which neither distorts space (left-right) nor time (forward-backward); the vertical axis is added merely for visualization. Space and time are distorted (dilated) in general relativity, but this is not the visualization to use to understand that.
To find the position of an object with no forces acting on it at some future time, we follow a straight path through spacetime from it’s location at the current time. Straight paths are defined as geodesics, meaning that left and right wheels spin at the same speed. But heavy objects warp spacetime, so that wheels nearer them need to roll up and down hills. Since the nearer wheel spends more motion going up and down, the farther wheel makes more progress forward, resulting in the geodesic curving toward the heavy object. This up-and-down idea is just a visualization; both space (x-axis) and time (y-axis) are unmodified.
Other forces, like the strong force and electromagnetic phenomena, do not warp spacetime but instead cause the cart to turn, one wheel spinning more than the other. The image wheels crossing gravitational bumps still works well in this scenario: even if the cart is turning, one wheel will still needs to travel more than the other.
Looking for comments…