|
Problem Set 2: Procedurally Predicting Presidential Primaries |
Out: 21 January 2004 Due: Monday, 2 February 2003, beginning of class |
Collaboration Policy - Read Carefully For this problem set, you are required to work with your assigned partner listed below. Partners were assigned (roughly) based on your answers to question 11 on the registration survey.
You and your partner should work together and turn in one assignment with both of your names on it. You should read the whole problem set yourself and think about the questions before beginning to work on them with your partner.
In addition to your partner, you may discuss this assignment with other students in the class and ask and provide help in useful ways. You may consult any outside resources you wish including books, papers, web sites and people except for materials from last year's CS200 course. If you use resources other than the class materials, indicate what you used along with your answer.
| Darryl Tyger Blackstock dtb9c@virginia.edu Dan Nguyen dvn4n@virginia.edu |
Redcliff Chen rc5p@virginia.edu Steven Jo smj9d@virginia.edu |
Chelsea Coleman cmc6d@virginia.edu TJ Ensele tje6n@virginia.edu |
Alexander Liu acl5f@virginia.edu Michael Owen Manning mom5v@virginia.edu |
| Henry Cook hmc3z@virginia.edu Stephen Sojka sps3b@virginia.edu |
Marija Cvijetic mc6sb@virginia.edu Preston Joseph Gisch pjg2m@virginia.edu |
Haben Ghermazien htg2j@virginia.edu William Ingram wai9z@virginia.edu |
Erin Paige Hallissy eph7y@virginia.edu Mee Kyung Hwang mkh7b@virginia.edu |
| R. Lincoln Hamilton rlh3x@virginia.edu Lauren Walker lew3p@virginia.edu |
Seth Kendler shk3m@virginia.edu Erika Vogel ekv2j@virginia.edu |
Susan R. Lindsay srl5u@virginia.edu Leah Nylen lan4d@virginia.edu |
Jonathan Carter jlc8eg@virginia.edu Kristina Hereford kah3j@virginia.edu Raquel Johnathan rdj2f@virginia.edu |
| Kathryn Morandi krm7d@virginia.edu Cristina Rabaglia cdr2m@virginia.edu |
Evong Nham en9j@virginia.edu Debora Wesner dtw4e@virginia.edu |
Nicole Numbers numbers@virginia.edu Benjamin Franklin Walter bfw6a@virginia.edu |
Purpose
- Become comfortable with procedures as parameters and results.
- Learn to define recursive procedures.
- Provide pragmatic policy pronouncements for presidential primary pretenders.
Background
Always vote for principle, though you may vote alone,
and you may cherish the sweetest reflection that your vote is never lost.
John Qunicy Adams
Although politicians in Adams' day may have always acted on principle, modern politicians tend to be more sophisticated, and modern voters more cynical. In this problem set we will look at the relatively new academic study of public choice economics. In economics, every individual or entity participating in a market (a place where products are bought and sold) looks to maximize its own utility (benefit derived from selling or purchasing a product). In a traditional market, consumers maximize their utility by maximizing the benefits gained from purchasing products, and producers maximize their utility by maximizing profits. In a political market, candidates for office serve as producers by formulating policy as their product, and voters serve as consumers by purchasing policy, which they do by voting for the candidate that formulated it.
Game theory attempts to explain how participants (or players) in a given market (or game) behave in order to maximize their own individual payoffs. Games are interesting because they analyze how players behave based on the actions of other players. While there are many types of games, we will start by looking at a very simple game based on the model of spatial competition:
Suppose there is a mile long boardwalk with patrons distributed equally and evenly across it. In addition suppose that all of these patrons are hungry and want to eat hot dogs. Two hot dog vendors, A and B, have decided to take advantage of this market by setting up mobile hot dog carts on the boardwalk. Their products are the same in every possible way, and the only way to differentiate between vendor A's product and vendor B's product is by looking at their position on the boardwalk. We assume that a patron will purchase a hot dog from the vendor that is nearest because the location of a vendor is the only way for a patron to decide to buy from one over the other. If vendor A and B are in competition with each other and they each want to maximize their individual revenue, where should A and B setup shop?

Since A wants to maximize the number of peope that will buy from her, and B wants to maximize the number of people that will buy from him, A and B each setup shop at the 1/4 and 3/4 marks, respectively, in order to split the market evenly. Interestingly enough, this initial setup is actually the most beneficial to the patrons as well. In a short matter of time, however, A will realize that she can get more customers by moving toward the 1/2 mark, since the patrons to the left of him must still go to him to buy a hot dog. In response to this, B will be forced to follow suit in order to keep up with A. Eventually, both A and B will find themselves in the center with the person at the 1/2 mark left to decide who gets the most business. This final setup is known as a Nash Equilibrium for this game, since no player can benefit anymore if the other player's position remains the same. (The Nash Equilibrium concept was discovered by John Nash, subject of A Beautiful Mind (winner of the 2002 best picture Academy Award), and winner of the 1994 Nobel Prize in Economics.)
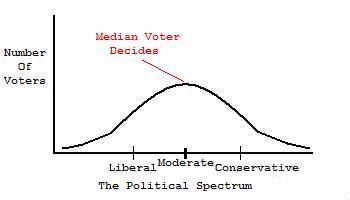
In 1957, Anthony Downs popularized the single-dimension policy space, or political spectrum, in his book An Economic Theory of Democracy. This spectrum, illustrated below, puts liberal policies on the left and conservative policies on the right. Downs also proposed a view of American voting procedures known as the Median Voter Theorem, that is similar to the hot dog game. It states that the median voter will decide an election between two candidates given a symmetric distribution of rationally-behaving voters along a one-dimensional political spectrum. As a consequence, candidates should move toward the center of the spectrum in an attempt to get the median voter's vote and win the election.
| Reading: Before going further, you should have finished reading all of SICP, Chapter 1 and GEB, Chapter 5. |
|
Downloads: Download this file to your
machine: ps2.zip
Create a folder called ps2 and unzip the contents into that folder. It contains four files:
Remember to make sure the Language is set to Full Scheme by selecting Language | Choose Language from the DrScheme menu. A dialog box will appear. Select Full Scheme in the Language choice menu and Pretty Big (MrEd and Advanced) in the right radio box. |
Drawing Points
We will find it useful to be able to draw a "game board" that will serve as the political spectrum. To start, we will learn how to draw points, then we will move onto curves. This will give us all we need to draw the game board.A curve is a (possibly infinite) set of points. We can draw a curve by mapping points on the curve to pixels on the screen.
For this assignment, we will use a coordinate system from (0, 0) to (1, 1):
| (0.0, 1.0) | (1.0, 1.0) | ||
|
|
|||
| (0.0, 0.0) | (1.0, 0.0) |
Points have x and y coordinates. To represent points we would like to define procedures make-point, x-of-point and y-of-point such that:
> (x-of-point (make-point 0.2 0.4)) 0.2 > (y-of-point (make-point 0.2 0.4)) 0.4Here's one way:
(define (make-point x y)
(lambda (selector) (if selector x y)))
(define (x-of-point point) (point #t))
(define (y-of-point point) (point #f))
The procedure make-point takes two parameters and returns
a procedure. The returned procedure is a procedure of one parameter,
selector. If the parameter is false (#f), it returns the
y parameter; otherwise it returns the x parameter.
We have provided some procedures for drawing on the window in curve.ss:
- (window-draw-point point) — Draw a black dot on the window at the point point. For example, (window-draw-point (make-point 0.5 0.5)) will place a black dot in the center of the window. (The point is only one pixel, so it is hard to see.)
- (window-draw-line point0 point1) — Draw a black line from point0 to point1. For example, (window-draw-line (make-point 0.0 0.0) (make-point 1.0 1.0)) will draw a diagonal line from the bottom left corner to the top right corner.
| Question 0: Define a procedure that uses make-point, window-draw-point and window-draw-line to draw a simple picture of a house. There is no need to make it as fancy as the White House. The point of this question is to get you acquainted with drawing objects on the screen. (You do not need to turn in anything for this question, but do not attempt the next question until you can do this.) |
Curves
Building upon points, we can make curves and lines (straight lines are just a special kind of curve). We can think of curves as procedures from values to points. One way to represent a curve is as a procedure that evaluates to a point for every value between 0.0 and 1.0. For instance,
(define (mid-line t)
(make-point t 0.5))
defines a curve that is a horizontal line across the middle of the
window. If we apply mid-line to a value x, we get
the point (x, 0.5). Hence, if we apply
mid-line to all values between 0.0 and 1.0, we get a
horizontal line.
Predict what (x-of-point (mid-line 0.7)) and (y-of-point (mid-line 0.7)) evaluate to. Try them in your Interactions window.
Of course, there are infinitely many values between 0.0 and 1.0, so we can't apply it to all of them. Instead, we select enough values to show the curve well. To draw a curve, we need to apply the curve procedure to many values in the range from 0.0 to 1.0 and draw each point it evaluates to. Here's a procedure that does that:
(define (draw-curve-worker curve t step)
(if (<= t 1.0)
(begin
(window-draw-point (curve t))
(draw-curve-worker curve (+ t step) step))))
(define (draw-curve-points curve n)
(draw-curve-worker curve 0.0 (/ 1 n)))
The procedure draw-curve-points takes a procedure representing
a curve, and n, the number of points to draw. It
calls the draw-curve-worker procedure. The
draw-curve-worker procedure takes three parameters: a curve,
the current time step values, and the difference between time step
values. Hence, to start drawing the curve, draw-curve-points
evaluates draw-curve-worked with parameters curve
(to pass the same curve that was passed to
draw-curve-points), 0.0 (to start at the first
t value), and (/ 1 n) (to divide the time values
into n steps).
The draw-curve-worker procedure is defined recursively: if t is less than or equal to 1.0, we draw the current point using (window-draw-point (curve t)) and draw the rest of the points by evaluating (draw-curve-worker curve (+ t step) step)).
The draw-curve-worker code uses the special form begin. The evaluation rule for begin is:
Evaluation Rule 4 - begin. To evaluate (begin Expression1 Expression2 ... Expressionk), evaluate each sub-expression in order from left to right. The value of the begin expression is the value of Expressionk.We stop once t is greater than 1.0, since we defined the curve over the interval [0.0, 1.0].
Question 1:
|
The Election Game
Our game will simulate an election for President of the United States. Each turn, all candidates will receive polling data and be able to adjust their positions on the political spectrum. Although our game is certainly not a perfect model of electoral politics, its better than Howard Dean's Dean for America game.For our game, we will need to represent a race consisting of an electorate and a set of candidates.
Modelling Electorates
The electorate models the views of the voters. Similar to a curve, an electorate is a procedure that takes a parameter representing a point on the political spectrum and evaluates to the number of voters at that point in the political spectrum. For our purposes, we don't need to worry about the total number of voters, it is sufficient to have an electorate that gives the relative distribution of voters. To make graphing easier, we will keep the actual value between 0.0 and 1.0.This defines flat-electorate as an electorate that is divided evenly through the political spectrum:
(define flat-electorate (lambda (pos) 0.5))We can turn an electorate into a curve by using the t parameter as the position and drawing the curve points as (t, (electorate t)):
(define (electorate-curve electorate) (lambda (t) (make-point t (electorate t))))And then draw the electorate using, (draw-curve-points (electorate-curve <electorate>) 1000).
In order for a candidate to make decisions about where to position herself, it will be useful to know properties of the electorate like how many voters there are between two positions. To estimate the number of voters, we will step through the electorate in a way similar to the way we step through a curve:
(define electorate-steps 1000) ;; number of samples through the electorate ;;; electorate-voters evaluates to the number of voters in electorate between ;;; start-position and end-position (define (electorate-voters electorate start-position end-position) (electorate-voters-worker electorate start-position end-position (/ 1 electorate-steps)))The electorate-voters-worker procedure should evaluate to the sum of the values of evaluating the electorate procedure at each step between start-position and end-position.
Question 3: Define the
electorate-voters-worker procedure used by
electorate-voters.
If your definition is correct, you should get results similar to these: |
Races and Candidates
A race is defined by an electorate and a list of candidate. For example, we can create a race to model a fictional election below (any resemblance to real elections or candidates is purely coincidendal):
(define iowa-caucus
(make-race
iowa-electorate
(list
(make-candidate "Kucinich" 0.05 static-candidate)
(make-candidate "Gephardt" 0.1 move-away-from-others)
(make-candidate "Dean" 0.2 move-away-from-others)
(make-candidate "Edwards" 0.6 move-towards-voters)
(make-candidate "Kerry" 0.8 move-away-from-others))))
Each candidate has a name, and current position (between 0.0 and 1.0),
and a reposition procedure that adjusts the candidate's position based
on polling data. The reposition procedure is a procedure that takes
two parameters: a candidate and polling data.
The reposition procedure should evaluate to a value that indicates how
the candidate is moving (negative values move the candidate to the
left, 0 stays at the current position, and positive values move to the
right). Note that a candidate who attempts to move too far on a
single day (that is, if a candidate procedure evaluates to a value
that is not in the range [-0.1, 0.1]) will be perceived as a
"flip-flopper", and will be eliminated from the race.
A simple candidate repositioning procedure represents a principled candidate (whose position is not swayed at all by polling data).
(define (static-candidate candidate poll) 0.0)Of course, principled candidates are unlikely to win, so we have defined two other candidate strategies in election.ss:
- move-towards-voters moves the candidate in the direction towards the most voters.
- move-away-from-others moves the candidate away from the other candidates.
We have defined the (run-one-day race) procedure that models one day of a race. The actual code in election.ss is quite complicated to deal with displaying results and illegal candidate moves, but here is the basic idea:
(define (run-one-day race)
(let ((poll-results (conduct-poll race)))
(make-race
(race-electorate race) ;; the electorate doesn't change
(map (lambda (candidate)
(candidate-set-position candidate
(+ (candidate-position candidate)
((candidate-reposition-procedure candidate)
candidate
race
poll-results))))
(race-candidates race)))))
It takes a race as a parameter, and evaluates to a new race.
It conducts a poll for the current candidate positions, and then
evaluates the candidate reposition procedure for each candidate.
Don't worry if you don't understand everything in
run-one-day, although you should recognize the map
procedure from Problem Set 1. In a few classes,
you will understand how to define procedures like map that
work on lists.
Since there may be any number of days before the election, we will need a procedure that can evaluate a procedure an arbitrary number of times.
|
Question 4: Define a procedure twice that composes a procedure with
itself. You should be able to use twice like this: (define run-two-days (twice run-one-day)) to define a procedure run-two-days that simulates two days of a campaign. Hint: Recall in Lecture 3 you saw the compose procedure that can be used to compose two functions that take one parameter:
(define (compose f g)
(lambda (x) (f (g x))))
|
|
Question 5: Define a procedure n-times that takes a
procedure and number n, and composes the procedure with itself
n times. Think about a recursive definition of
n-times: to apply a procedure 1 time, just apply the procedure;
to apply the procedure n times, compose the procedure with the
result of applying the procedure n - 1 times. (See the hint below for help.)
Hint: Your procedure will look like this (the parts in < ... > brackets are what you need to fill in):
(define (n-times f n)
(if (= n 0)
(lambda (x) x) ; No procedure applications, return the identity procedure
(compose <fill this in>
(n-times f <fill this in>))))
|
We have defined a procedure run-election that uses the n-times procedure you have defined to run an election:
(define (run-election race number-of-days)
(let ((final ((n-times run-one-day number-of-days) race)))
(let ((final-votes (conduct-poll final)))
(display-poll-results final final-votes)
(display-winner final final-votes))))
The important part is the application of n-times (in bold). The
rest of the procedure is used to record the final race, and then display
the results.
When you evaluate (run-election iowa-caucus 20) you will be able to see the candidates move around on the display and the polling results in the interactions window. The blue line across the display shows the electorate, and the vertical line for each candidate shows their latest polling results. At the end of the execution, you should see:
(Please recall that any resemblence to real elections is purely coincidental.)======================
Final Election Results
======================
Candidate Kucinich at 0.05: 0.08132666666666673
Candidate Gephardt at 0.17000000000000007: 0.11200000000000003
Candidate Dean at 0.3000000000000001: 0.17974000000000004
Candidate Edwards at 0.49999999999999994: 0.19163333333333343
Candidate Kerry at 0.5999999999999999: 0.4352999999999997
The winner is: Kerry
For the final question, your task is to define a candidate repositioning procedure that will help you win the CS200 primary:
(define cs200-primary
(make-race
flat-electorate
(list
(make-candidate "Alyssa P. Hacker" 0.4 static-candidate)
(make-candidate "Ben Bitdiddle" 0.1 move-away-from-others)
(make-candidate "Cy D. Fect" 0.9 move-away-from-others)
; add your candidate: (make-candidate "YOUR NAME" your-position-value your-repositioning-procedure)
)))
|
Question 6: Define a winning candidate repositioning procedure
that can win the election (run-election cs200-primary 20). |
Competition
You can each a "Gold Star" on this assignment without going any further. More ambitious students will want to develop a candidate procedure that can compete with other student's candidate procedures to win an election. We will provide more details on the competition next week. Submit your candidate using the Candidate Submission Page.Discussion
The Downsian Model helps explain why third parties have a difficult time getting traction in US politics — a third party candidate draws votes away from the major party candidate whose views are most similar to the third party candidate's. Hence, the result of a strong third party candidate is to ensure that the major party candidate furthest from the third party candidate will win, therefore discouraging future support for third party candidates.The Virginia Democratic Primary is February 10. Since Virginia is an open primary state, you may vote in the primary regardless of your political affiliation. Strategic voters who prioritize the general election result will vote positionally for the candidate that they think candidate they will have the best chance to win the general election (or to lose the general election if you want the Republicans to win the general election). Ironically, the Downsian model would suggest that liberals should vote for the most conservative candidate (who would have the best chance to defeat Bush in the general election), and conservatives should vote for the most liberal candidate (who would have the worst chance to defeat Bush in the general election). Of course, if you follow Adams' advice and vote on principle, you won't need to worry so much about modelling the general electorate.
If you are from Arizona, you might want to vote for Oksana Komarnyckyj, who's campaign is managed (and website developed) by a CS200 graduate and former assistant coach.
| Credits: This problem set was developed for UVA CS200 Spring 2004 by Andrew Connors with help from Sarah Bergkuist, David Evans and Katie Winstanley. |