| Exam 1 Comments |
Out: 10 September 2002 |
Average: 77.1
Specifying Procedures
1. (8.7 average out of 10) Muddle B. Fuddle wants to add a deleteName method to the StringTable class from Problem Set 3 (http://www.cs.virginia.edu/cs201j/problem-sets/ps3/StringTable.spec):
public class StringTable
{
// overview: StringTable is a set of <String, double> entries,
// where the String values are unique keys. A typical StringTable
// is {<s0: d0>, <s1: d1>, ... }.
//
...
}
Muddle is planning to use a Vector of String, value record pairs to represent his
StringTable.
He suggests this specification:
public boolean deleteName (String name) // REQUIRES: The parameter name is not null. // EFFECTS: Goes through the entries in the elements Vector, and removes // the one whose key matches name.Identify at least three important problems with Muddle's specification and explain why each problem is bad.
There are dozens of problems with Muddle's specification! The most important are:2. (7.7 / 10) Write a good specification for the deleteName method.
- It is written in terms of the concrete representation, not the abstract type. Specifications should not be tied to particular implementations.
- It is written in an operational (how) way ("goes through"). Specifications should be declarative (explain what it does, not how).
- It is missing a modifies clause. Based on its name and effects clause, it should modify the this object.
- Its postcondition does not explain what happens in all situations: what if the name is not in this? what is it is in the elements Vector more than once? (Of course, if the specification were written in terms of the abstraction, this wouldn't be a problem.)
- The method header has a boolean return type, but the effects clause does not explain what this type means.
public boolean deleteName (String name) // REQUIRES: The parameter name is not null. // MODIFIES: this // EFFECTS: If name matches a key in this, removes the entry // associated with that key and returns false. Otherwise, // does not modify this and returns true.We could also describe its behavior using our abstraction notation:e.g., If this_pre = { <s0: d0>, <s1: d1>} and s0 equals name, result == true and this_post == { <s1: d1>}. If name does not equal s0 or s1, then result == true and this_post == this_pre.
Data Abstractions
3. (8 / 10 (this was listed as being 7 points on the exam, but I graded it out of 10) As specified above, is WDGraph likely to be a useful abstraction? If so, explain briefly an application that could use it. If not, explain what methods must be changed or added to make it useful.
The most obvious problem is there is no method to get the weight associated with an edge. Without this, the abstraction isn't adequate — we would be better using a normal Graph without edge weights. So, we should add a method getEdgeWeight:4. (7.8 / 10 (listed as 8, but graded out of 10) As specified, WDGraph is a mutable type. Explain what changes would be necessary to make WDGraph an immutable type instead, and identify at least one good reason why we might prefer the immutable version.public int getEdgeWeight (String fnmode, String tnode) throws NoNodeException // EFFECTS: If fnode or tnode is not the name of a node in // this.nodes, throws NoNodeException. Otherwise, if // there is an edge from fnode to tnode in the graph, // returns the weight of that edge. If there is no // edge, returns 0.Note that this.nodes in our specification means the abstract nodes set used in the overview, not anything to do with our rep (which happens to use nodes also). Perhaps, our specification should throw an exception if the node does not exist instead of returning 0.To be useful, the abstraction should have some more observers: getNeighbors (returns an iterator that yields the neighbors of a node), and perhaps nodes (returns an iterator that yields all the nodes in the graph).
For some purposes, it would be more useful to be able to have zero-weight edges (but there are plenty of applications that can use the abstraction with this restriction).
To be immutable, the type must not provide any mutators. So, we would need to remove the addNode and addEdge methods. If we just removed them, we would have an immutable datatype, but it wouldn't be useful. All we could do is create an empty graph and call the observers on it. So, we need to either:5. (10.1 / 15) Suppose we decide to implement WDGraph using this rep:
- Provide a constructor that can create a particular graph (for example, by reading it from a file).
- Or, provide producer versions of the addNode and addEdge methods. Instead of modifying the this object, these methods would create and return a new graph (with the additional node or edge).
Possible advantages of making WDGraph immutable are that it makes it easier to reason about code (we don't need to worry about aliasing). A disadvantage is that implementing addNode and addEdge as producers instead of mutators will make them more complicated and require extra storage (creating all those new graphs) and computation (copying).
// Rep:
String nodes[];
int edges[][];
// Abstraction Function:
// AF (c) = < nodes, edges > where
// nodes = { c.nodes[i] | 0 < i <= c.nodes.length }
// edges = { < c.nodes[fi], c.nodes[ti], c.edges[fi][ti] > |
// 0 < fi <= c.nodes.length,
// 0 < ti <= c.nodes.length
// where c.edges[fi][ti] != 0
//
// For example, the representation below would represent the flight
// graph described in the overview:
//
// c.nodes = [ "Charlottesville", "Dulles", "Richmond" ]
// c.edges = [ [ 0, 119, 89],
// [ 139, 0, 0 ],
// [ 0, 79, 0 ]
//
The hasEdge method is implemented as:
private int lookupNode (String node) throws NoNodeException
// EFFECTS: If node is a node in this.nodes, returns the
// index such that this.nodes[result].equals (node).
// Otherwise, throws NoNodeException.
// (Note that lookupNode is a private method. Hence, it is okay that we
// have specified it using the concrete representation instead of in
// terms of the abstraction.)
public boolean hasEdge (String fnode, String tnode)
throws NoNodeException {
return (edges[lookupNode (fnode)][lookupNode (tnode)] != 0);
}
What rep invariant would be necessary to make this implementation
correct?
The best way to think about this is to look at the code for hasEdge and determine what needs to be true for it to work:return (edges[lookupNode (fnode)][lookupNode (tnode)] != 0);We are indexing the edges array, so it must not be null://@invariant edges != nullWe are calling lookupNode. It has no require clause, though, so nothing has to be true for this to be okay.We are indexing edges[lookupNode (fnode)]. For this to be in bounds, we need to know that the result of lookupNode (fnode) is between 0 and the length of edges - 1. The effects clause for lookupNode tells us that its result is a valid index of the nodes array, hence it is between 0 and nodes.length - 1. From this, we can infer that the edges array must have at least as many elements as the nodes array:
//@invariant edges.length >= nodes.lengthNext, we index in the second array: edges[lookupNode (fnode)][lookupNode (tnode)]. So, edges[lookupNode (fnode)] must not be null. Further, the length of each edges[i] array must be >= nodes.length:// invariant forall 0 <= i < nodes.length // edges[i] != null // edges[i].length >= nodes.lengthThat's all we can definitively say about the rep invariant from just looking at what is necessary for hasEdge. It is likely that lookupNode will require the nodes array contain no duplicates.
Testing
6. (8.4 / 10) What would be a reasonable set of black box test cases to the addNode method?
The important thing to remember about black box test cases is that they are based on the specification, not a particular implementation. We should test all paths through the specification of addNode:// EFFECTS: If node is the name of a node in this.nodes, // throws the DuplicateNode exception. Otherwise, // adds a node named name to this: // this_post = < this_pre.nodes U { node }, this_pre.edges >There are two obvious paths:Reasonable test cases would be:
- The node already exists in the graph.
- The node does not already exist in the graph.
WDGraph g = new WDGraph (); g.addNode ("Charlottesville"); g.addNode ("Dulles"); g.addNode ("Dulles"); // should throw DuplicateNodeExceptionWe should also test boundary or special cases: the node is null, and the graph is empty.
7. (6.9 / 10) Suppose we implement addNode as below. What additional glass box test cases (if any) are necessary?
public void addNode (String node) throws DuplicateNodeException {
try {
lookupNode (node);
throw new DuplicateNodeException (node);
} catch (NoNodeException e) {
String [] oldnodes = nodes;
nodes = new String [oldnodes.length + 1];
for (int i = 0; i < oldnodes.length; i++) {
nodes[i] = oldnodes[i];
}
nodes[oldnodes.length] = node;
}
}
The glass box test cases should excercise paths through the
implmentation. One path is when lookupNode does not throw a
NoNodeException. Our black box test cases already cover this
when we add a duplicate node. Another path is when lookupNode
throws an exception and we execute the catch block. This block
has essentially infinitely many paths through the loop — we can't
test them all, but we should test it for 0, 1 and several iterations.
The first addNode black box test cases tests it for 0, the
second tests it for 1. We need some additional tests to test it for
several:
WDGraph g = new WDGraph ();
g.addNode ("Charlottesville");
g.addNode ("Dulles");
g.addNode ("Richmond");
g.addNode ("Reagan");
8. (4.7 / 10) What is the serious flaw with our addNode implementation?
The really serious flaw is that it does not preserve the rep invariant. Among other things, our rep invariant requires: edges.length >= nodes.length. The implementation of addNode increases nodes.length by 1. We need to increase edges.length by 1 also to preserve the rep invariant. This makes sense — addNode should extend each edges array by 1 so that edges involving the new node can be stored. Note that our addNode tests would not reveal this problem. It only becomes apparent when we call a method like hasEdge that depends on the edges array satisfying the rep invariant.Another possible flaw is the code does not address what happens if node is null. The lookupNode specification implies that nodes in the graph cannot be null, but does not have a requires that node is not null. As specified, it would throw the NoNodeException if node is null (but a better lookupNode spec would make this much more clear). Hence, if addNode is passed a null node, it would add it to the array, which would violate the rep invariant. The best solution to this is probably to just add requires node != null to the specification for addNode.
Design
9. (14.6 / 20) Due to recent budget cuts at the University, SEAS has decided to replace the student advising office with a computer program. The program will take student course selections as input and either approve or disapprove of the course selections based on whether or not the student has satisfied the necessary prerequisites. (Note: the advising office does many other useful things too, of course. The administration is still working on ways to replace those functions with programs.)All courses have a department mnemonic (e.g., "CS") and course number (e.g., 201). (As a further cost saving measure, the administration has decided to eliminate deviant courses that have extra modifiers after the number so you don't need to worry about handling courses with names like "CS201J".) Courses also have a name that purports to describes their content (e.g., "Engineering Software").
The program will use a database with information on courses and their prerequisites. A course may have no prerequisites, or may have multiple prerequisites or alternate prerequisites. For example, the prerequisites for "CS201: Engineering Software" are "either CS101: Intro to Computer Science OR CS200: Computer Science from Ada and Euclid to Quantum Computing and the World Wide Web". The prerequisites for "UBW101: Underwater Basketweaving" are "SCU101: Scuba Diving AND (either ART253: Introduction to Basketweaving OR SPD101: Weaving Webs for Poets)".
You've been hired to design the prerequisites checking program. Describe your design using a modular dependency diagram, and a brief description that describes each of the modules in your design. If a module is an abstract data type, write an overview specification of the data type and identify important methods (but you do not need to specify them). Explain a brief strategy for implementing and testing your design.
Your answer should clearly identify the data abstractions in your design, but you need not explain how they will be implemented. Your answer to this question should not require more than two pages (but if you really want to say more than that, its better to use more pages than to write really small).
Our design uses these abstractions:The main module, Advisor will provide a method that takes as input a CourseSet describing the courses a student wants to take and a CourseSet that contains the courses the student has already taken, and produces output on the display that indicates if any courses have prerequisites that are not satisfied by the student. Realistically, the set of courses the student has taken would be obtained from a database by looking up from the student's ID. So, we should provide abstractions for the database and student record:
- Course — immutable abstract type for representing a course. Includes it name, mnemonic and number, as well as the prerequisites for that course.
- CourseSet — a set of courses.
- Prerequisites — immutable abstract type for representing prerequisites. Prerequisites can be a single course, an AND of two prerequisites, or an OR of two prerequisites (note these are defined recursively to support nested AND and OR prerequisites). Prerequisites implements a method boolean isSatisfied (CourseSet courses) that returns true iff the courses in the CourseSet satisfy the prerequisites.
Our module dependencies are:
- StudentDatabase — datatype for interacting with the student database. Provides a method that returns the StudentRecord associated with a student's ID.
- StudentRecord — record with information on what courses a student has taken.
A good implementation strategy would be to divide the work into: 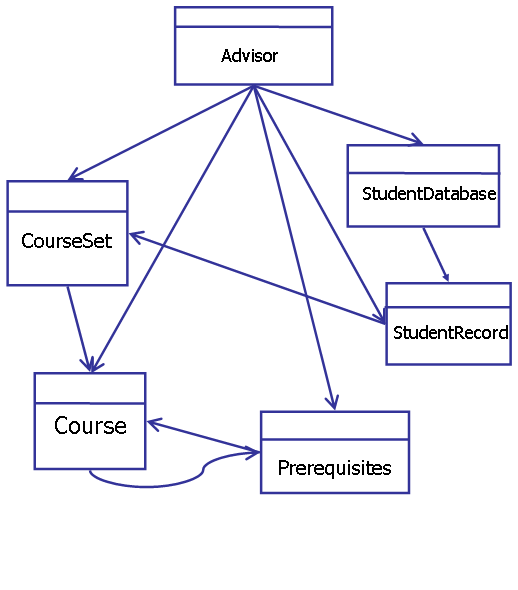
You didn't need to provide an implementation, but we could implement Prerequisites like this:
- Developing and testing the prerequisites checking module which will be the trickiest part to code and test, but can for the most part be tested using stub classes for everything else (for example, before Course and CourseSet are done, we could test our prerequisites modules using String and StringSet).
- Developing and testing the other modules.
abstract public class PrerequisitesTerm { abstract public boolean satisfies (CourseSet c); } public class SingleCourseTerm extends PrerequisitesTerm { private /*@non_null@*/ Course c; public SingleCourseTerm (Course c) { this.c = c; } public boolean isSatisfied (CourseSet c) { return c.contains (c); } } public class AndPrerequisite extends PrerequisitesTerm { private /*@non_null@*/ Prerequisites term1; private /*@non_null@*/ Prerequisites term2; public AndPrerequisite (/*@non_null@*/ Prerequisites p, /*@non_null@*/ Prerequisites q) { term1 = p; term2 = q; } public boolean isSatisfied (CourseSet c) { return p.isSatisfied (term1) && q.isSatisfied (term2); } public class OrPrerequisite extends PrerequisitesTerm { private /*@non_null@*/ Prerequisites term1; private /*@non_null@*/ Prerequisites term2; public OrPrerequisite (/*@non_null@*/ Prerequisites p, /*@non_null@*/ Prerequisites q) { term1 = p; term2 = q; } public boolean isSatisfied (CourseSet c) { return p.isSatisfied (term1) || q.isSatisfied (term2); } public class Prerequisites { private PrerequisitesTerm term; public Prerequisites (PrerequisitesTerm term) { this.term = term; } public boolean isSatisfied (CourseSet c) { return term.isSatisfied (c); } }