Problem Set 4: Tree of Life (Designing with ADTs)

Out: 19 September 2002 Design Document Due: Thursday, 26 September 2002, before class Due: Thursday, 3 October 2002, before class

Collaboration Policy (read carefully)

For this problem set, you are required to work with an assigned group. Unlike other assignments, your group should strive to divide the work in such a way that you can work independently on different parts, and combine your work to solve the problem. In your design document, you will document each member's role. The groups were assigned based on alphabetical order by first name:

Lee Alex Wiygul Alicia Connors Andrew	Barrett Brian Croft Tucker Huntley Daniel	Eaton Darnell Lee Diane Wu Doris	Lucas Erin Assanah Fayekah Chung Helen	Fournier Jacques Franchak John Lin Joyce
Guttridge Katherine Winstanley Katie Dennehy Kevin	Aimone Laura Seirafi Reza Rose Sarah	Geyer Scott Hoon Sherlynn Stockdale Spencer	Lai Wei-Han Rutherford William Christopher Zhang Zhannan

Reading: Chapter 13 (except Section 13.11, we won't cover Data Models).

Purpose

• Learn to solve a problem by designing using data abstractions.
• Learn to design and implement data abstractions.

In Problem Set 3, you implemented a data abstraction given a specification. In this assignment, you will design and implement several data abstractions to solve a complex problem. It is up to you to decide what those data abstractions are.

Phylogeny

Phylogeny is the problem of classifying items according to their relationships. A phylogeny of life shows how different species evolved from common ancestors. A phylogeny of language shows how different languages evolved from a common language. We can visualize a phylogeny as a tree, for example, here is a phylogeny of Ichthyosaurs:

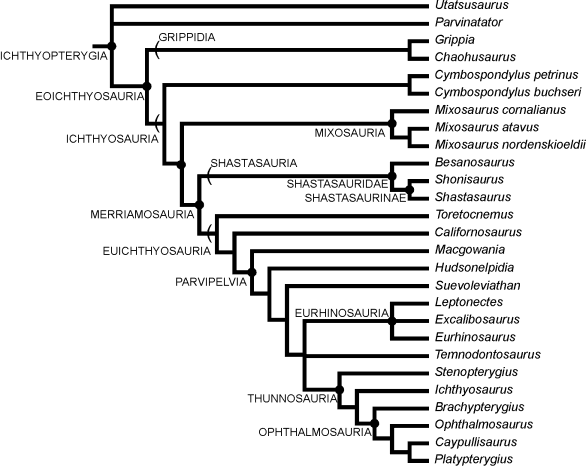Phylogeny of Ichthyosaurs (from UC Berkeley's Museum of Paleontology)

The way biologists (or linguists) determine evolutionary relationships is to look for similarities and differences between species (or languages). This is done by identifying a set of features that describe properties of a species or language. For species, the features might be phenotypic properties (e.g., do organisms have wings or gills?) or genotypic properties (the DNA sequence). Genotypic properties are likely to produce more accurate results, since small changes in genomes can produce large phenotypic changes.

If two species have similar genomes, it is likely they evolved from comon ancestors. Biologists measure the similarity of genomes based on the number and likelihood of different kinds of mutations — base pairs may be inserted, deleted, duplicated, moved, or substituted. The number of mutations necessary to match two genomes gives an indication of the likelihood that the species evolved from a common ancestor. For this assignment we will assume a very simple model: the only mutation is a substitution or a single base pair and all substitutions are equally likely.

One measure of which tree is the most likely to represent the actual evolution of a set of species is parsimony. The parsimony principle is that if there are two possible explanations for an observed phenomenon, the simpler explanation is most likely to be correct. In producing phylogenetic trees, parsimony means we should look for the tree that requires the fewest possible total number of mutations. We model this by counting each substitution mutation as 1, and selecting the tree that minimizes the total number of mutations.

For example, consider the set of species described by the genomes below (note: of course, these are not their real genomes!):

Cat	catcat
Tiger	catgat
Leopard	tatgat

Suppose we know Cat is the common ancestor of all the species. The difference between a Cat and a Tiger is one point mutation (change the second c to a g). The difference between a Cat and a Leopard is two point mutations (change the first c to a t and the second c to a g). So, the phylogeny tree:

              Cat
              / \
             /   \
          Tiger  Leopard

would have a parsimony score of 3 (1 for the Cat → Tiger evolution and 2 for the Cat → Leopard evoluation). An alternate tree:

             Cat
              |
              | 
            Tiger
              |
              |
           Leopard

would have a parsimony score of 2 (1 for the Cat → Tiger evolution and 1 for the single point mutation necessary to evolve the Tiger into a Leopard). Thus, our data would support the conclusion that the second tree is more likely, and the Leopard evolved from the Tiger, instead of the Leopard and Tiger both evolving from the Cat independently.

Problem

Your task is to produce a program that takes as input a list of species and their genomes, and produces as output a phylogeny tree that minimizes the total number of mutations. For simplicity, you may assume:

• Only substitution mutations occur, and each single base change is equivalent (the parsimony score between any two species is a count of the number of bases that are different in their genomes).
• Every species has zero, one or two evolutionary descendants (the tree is binary).
• The first species in the input file is the common ancestor of all other species in the file (the root of the tree).

You may also assume the input file is complete (there are no missing species). Note that if it were not, it may be possible to produce a lower parsimony score by inventing a new common ancestor. For this assignment, the tree you produce should only include species in the input file.

The input file contains lines of the form: species genome. The species is a sequence of non-white space characters that provides an indentifying name for a species. The genome is an encoding of the features of that species. There are one or more spaces between the species and genome. For the examples, we will use genomes that look like DNA sequences, but your program should work on any genome that is a sequence of characters.

Your output should present a phylogeny tree for the input species that minimizes the total number of mutations. You should display your output tree as indented text, where species on the same level of the tree are indented the same number of spaces. For the Cat, Tiger and Leopard example above, your program should produce:

Cat [catcat]
   Tiger [catgat]
      Leopard [tatgat]
Total mutations: 2

For the input file:

Aphid       aagctatac
Bat         attacatag
Cat         aagctacat
Duck        attaattat
Elephant    attaatgac
Fly         attaattac

your program could produce:

Aphid [aagctatac]
   Bat [attacatag]
      Fly [attaattac]
         Elephant [attaatgac]
         Duck [attaattat]
   Cat [aagctacat]

Parsimony value: 12

This corresponds to the (not biologically correct!) tree:

                 Aphid
                  / \
                 /   \
              Bat    Cat
               |
               | 
              Fly
              / \
             /   \
       Elephant  Duck

Note that there may be several possible trees with the same parsimony score. For example, these trees also have parsimony scores of 12:

Aphid [aagctatac]                              Aphid [aagctatac]
   Bat [attacatag]                                Fly [attaattac]
      Duck [attaattat]                               Elephant [attaatgac]
         Fly [attaattac]                             Duck [attaattat]
            Elephant [attaatgac]                        Bat [attacatag]
   Cat [aagctacat]                                Cat [aagctacat]

If there are different phylogeny trees that have the same parsimony score, your program may produce any one of those trees, so long as it produces a tree with the minimum parsimony score.s

Finding Trees

To find the best phylogeny tree, we can generate all possible trees and calculate the parsimony score of each tree. This approach will be satisfactory for the small species sets we will use for this assignment. The amount of work required with this approach grows exponentially with the number of species, so the number of possible trees quickly becomes huge:

Number of Species		Number of Possible Trees
2		1
3		3
4		15
5		108
6		1020
7		11970
8		168210

For large sets of species, it is not possible to try all possible phylogeny trees. Hence, computational biologists study techniques to approximate finding the best tree without having to examing all possible trees.

Note that we consider the left and right children to be symmetric. That is,

           A                                       A
          / \        is the same tree as          / \
         B   C                                   C   B

For this assignment, we will limit the number of species your program must work on to 7. So, it is reasonable to generate all possible trees and find the most parsimonious phylogeny.

Generating all possible trees can be thought of as a recursively:

• Pick a root
• Consider all possible ways of partitioning the remaining nodes into the left and right sides of the tree
• For each partition, produce all possible trees with that set of nodes

We can describe the tree-finding algorithm with the pseudocode below:

   // Produces all possible binary trees containing all the nodes.
   allPossibleTrees (nodes) {
      if nodes is empty return { }
      if nodes has one element e
         return { Tree with e as root and no children }
      
      // Make each element the root in turn, and produce all possible
      // trees with that element as root.
      result = { }
      for each element, root of nodes 
         result = result U allPossibleTreesRoot (root, nodes - root)
   }

   // Produces all possible binary trees with root as the root and all
   // the nodes as descendants.
   allPossibleTreesRoot (root, nodes) {
         result = { }
         // splits is a collection of <left: set, right: set> pairs 
         // for all possible divisions of nodes into two partitions
         splits = allPossibleDivisions (nodes)

         for each element, split of splits 
            lefttrees = allPossibleTrees (split.left)
            righttrees = allPossibleTrees (split.right)
            
            for each element, lefttree of lefttrees
                if righttrees is empty
                   result.insert (tree with root as the root and lefttree as its left child) 
                else
                   for each element, righttree of righttrees
                      result.insert (tree with root as the root, 
                                     lefttree as its left child and righttree as its right child)

         return result
   }

The allPossibleDivisions procedure produces a set containing all possible ways of partitioning a set into two groups. An easy way to do this is to take advantage of binary numbers. A 0 in the i^th place indicates that the i^th element of the set should be in the left partition; a 1 in the i^th place indicates that the i^th element of the set should be in the right partition. For example, if our set is {A, B, C}, we can count in binary up to 2³ - 1 to enumerate all possible partitions:

Count   Binary     Left Partition    Right Partition
0       000        { A, B, C }       { }
1       001        { A, B }          { C }
2       010        { A, C }          { B }
3       011        { A }             { B, C }
4       100        { B, C }          { A }
5       101        { B }             { A, C }
6       110        { C }             { A, B }
7       111        { }               { A, B, C }

Since we consider the left and right partitions indistinguishable, we only need the first four of these.

The java.math.BigInteger (follow the link for the specification) class will probably be useful for implementing this.

Design Document

A design document is due on Thursday, 26 September. It should contain:

• A modular dependency diagram showing the classes you will use to implement your solution.
• Specifications of those classes. All your class specifications should include an overview (that describes the data abstraction, its mutability, and introduces an abstract notation) and specifications for the public operations of the class.
• Descriptions of your representations, rep invariants and abstraction functions for those classes.
• Work division. Description of who will implement each class in your design, devise unit testing strategies and test cases for each important class, and devise integration testing strategies and test cases.

Final Report

On Thursday, 3 October turn in a final report containing:

• The four parts of your design document, with explanations of any changes between your proposed design and the final design:
  • A modular dependency diagram showing the classes you will use to implement your solution.
  • Specifications of those classes. All your class specifications should include an overview (that describes the data abstraction, its mutability, and introduces an abstraction notation) and specifications for the public operations of the class.
  • Work division. Description of who will implement each class in your design, devise unit testing strategies and test cases for each important class, and devise integration testing strategies and test cases.
  • Descriptions of your representations, rep invariants and abstraction functions for those classes. If you changed your mind about any of the representations since the design document, explain why.
• All the code you wrote to implement your program. Each class implementation should include a rep invariant and abstraction function, documented in comments in the code. Your code should be annotated with ESC/Java annotations, and checked by ESC/Java.
• An explanation of how you tested your code. This is not a list of all the test cases you tried, but an explanation of what you did to validate your code. Include any interesting programs you developed to help your testing.

Submit Code

Credits: This problem set was developed for UVA CS 2001J Fall 2002.

University of Virginia Department of Computer Science CS 201J: Engineering Software

Sponsored by the National Science Foundation

cs201j-staff@cs.virginia.edu