| Exam 2 - Answers |
Out: 5 April 2002 Due: Wednesday, 10 April 2002, 11:00AM |
Each question is worth 10 points.
| Question | Average | Question | Average |
|---|---|---|---|
| 1 | 8.3 | 2 | 8.9 |
| 3 | 8.1 | 4 | 7.1 |
| 5 | 7.9 | 6 | 7.6 |
| 7 | 9.6 | 8 | 9.2 |
| 9 | 6.8 | 10 | 5.8 |
| Total | 79.2 | ||
If the sum of your scores on exam 1 and exam 2 is at least 140, and you get more than 5 on every problem set (including PS8), you are guaranteed at least a B in the class.
State and Mutation
1. After evaluating (define spair (cons 1 2)), we can draw spair as:
| 1 | 2 |
Draw spair after then evaluating (set-car! spair spair).
Answer: Evaluating (set-car! spair spair) replaces the car of the cons cell with the value of spair, which is the cons cell. Hence, we get a pointer to the cons cell like this:2. Give a sequence of two Scheme expressions that would produce the global environment shown below after they are evaluated:
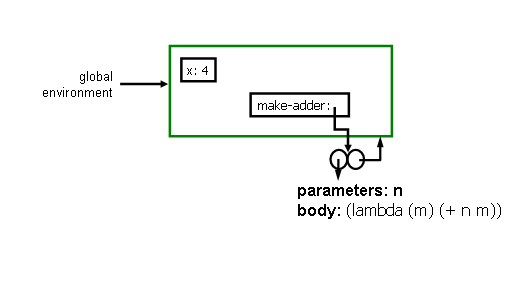
Answer:3. After evaluating the two expressions from the previous question, what one additional expression could you evaluate to make the environment look like:There is a straightforward mechanical transformation from the environment picture to the procedure definition. The parameters came from a lambda, and the body is the body inside the lambda.(define x 4) (define make-adder (lambda (n) (lambda (m) (+ n m))))
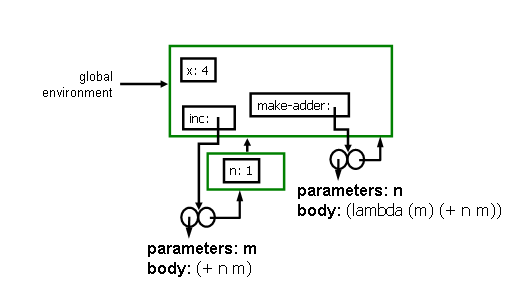
Answer: The simplest expression to evaluate is (define inc (make-adder 1)). Because there is a new frame, you know there must have been an application. When we apply make-adder it creates a new frame with a place named n (the parameter). The value in that place is what we apply make-adder to. The body is evaluated in the new envrionment, to produce the procedure as shown in the environment diagram.
Problem Classifications
4. The Grammar Checking ProblemInput: A BNF grammar G and a string S
Output: true if S is a string in the language described by G, false if S is not a string in the language.
Answer: This is decidable. The string S is a finite sequence of characters. The dumb way to check if the string is in the grammar G is to generate all possible strings in the grammar of length S and see if one of them matches S. We can measure the side of the problem in terms of the length of S (n), the number of letters in the alphabet (A), and the number of rules in the grammar G (g). There would be An possible strings of length n, we can check is a given string matches S quickly. So, it is in NP. In fact, it is also in P since there are clever algorithms we can use that go backwards instead of trying all possible strings in the grammar. Based on the characters in S, we know the possible sequences of non-terminals. Then, we can follow the grammar replacement rules backwards to see if we get to the starting production in the grammar. (Seeing this is pretty tricky — you got full credit for a good argument that it was decidable.)5. The Expression Equivalence Problem
Input: Two typed mini-Scheme (the language from classes 28 and 29) expressions, S and T
Output: true if S and T evaluate to the same value, false otherwise.
Answer: This is undecidable. We cannot just evaluate S and T, since they may not halt (we don't know how long to wait before giving up). The cleverest proof was Jacques Fournier's:6. The Type Equivalence ProblemSince programs that don't halt have no value, we assume (same-value? P P) is false for a program that doesn't halt. (This is a little bit dangerous unless we are very precise about what same-value? means.) Then, if P halts, it always produces the same value (P must be a function).(define (halts? P) (same-value? P P))
Input: Two typed mini-Scheme (the language from classes 28 and 29) expressions, S and T
Output: true if S and T have the same type, false otherwise.
Answer: This is decidable. In fact, you have a program that does just that — the typeof procedure! This procedure is O(n) where n is the number of sub-expressions in S and T. So, it is in P.
Evaluators
For questions 7-10, you will modify the Typed Mini-Scheme evaluator from classes 28 and 29.
Typed Mini-Scheme does not support the begin special form. In questions 7 and 8, you will extend it to handle (begin expression1 expression2). The begin special form takes two expressions. It evaluates expression1 first, and then evaluates expression2. The value of the begin is the value of expression2. The type of the begin is the type of the expression2.
| For the code you turn in for questions 7-10, make sure to clearly identify the code for each question. Don't include code from clueval.ss that you did not change at all, but remember to include all of your changes. If you are not able to get all the code working, you can still get substantial credit for these questions by explaining what you are trying to do, turning in the code you have written so far, and explaining what you think is going wrong. |
Downloads:
- http://www.cs.virginia.edu/cs200/exams/clueval.ss — Typed mini-scheme evaluator from classes 28 and 29. modified to support abstract types (as described in questions 9 and 10). You do not need to be concerned with the modifications for questions 7 and 8.
- http://www.cs.virginia.edu/cs200/exams/listprocs.ss — Unchanged from PS7
- http://www.cs.virginia.edu/cs200/exams/assert.ss — Unchanged from PS7
To evaluate begin we need to add a new evaluation rule to meval:8. Extend typeof to check the type of begin special forms.(define (begin? expr) (tagged-list? expr 'begin)) (define (begin-expr1 expr) (cadr expr)) (define (begin-expr2 expr) (caddr expr)) (define (meval expr env) (cond ... ((begin? expr) (begin (meval (begin-expr1 expr) env) (meval (begin-expr2 expr) env))) ... ) )
Answer: The type of (begin expr1 expr2) is the type of expr2, but we also need to check the type of expr1. Here is the code we added to typeof:(define (typeof expr env) (cond ... ((begin? expr) (begin (typeof (begin-expr1 expr) env) (typeof (begin-expr2 expr) env))) ... ) )
Up and Down
See exam2.html for the question background and A History of CLU, Barbara Liskov, 1992 for more background on CLU.9. Extend typed Mini-Scheme to support the special form (up Type Expr). An up expression converts the value Expr evaluates into a value of abstract type Type. The value of (up Type Expr) is the value of Expr. The type of (up Type Expr) is the abstract type named by Type. It is a type error if the representation type of Type does not match the type of Expr.
Remember you will need to change both typeof and meval.
Answer: Evaluating up is just evaluating the value in the up expression:10. Extend typed Mini-Scheme to support the special form (down Type Expr). A down expression converts the value Expr evaluates to into a value of the representation type of the abstract type Type. The value of (down Type Expr) is the value of Expr. The type of (down Type Expr) is the representation type of the abstract type named by Type. It is a type error if the type of Expr does not match the abstract type named by Type.To type check an up expression, we need to check that the type of the expression matches the representation type of the abstract type named in the up expression:(define (up? expr) (tagged-list? expr 'up)) (define (up-type expr) (cadr expr)) (define (up-expr expr) (caddr expr)) (define (meval expr env) (cond ... ((up? expr) (meval (up-expr expr) env)) ... ) )(define (typeof expr env) (cond ... ((up? expr) (typeof-up expr env)) ... ) ) (define (typeof-up expr env) (let ((exptype (typeof (up-expr expr) env)) (reptype (environment-lookup-value (up-type expr) env))) (if (type-match exptype reptype) (make-abstract-type (up-type expr)) (begin (printf "Up type error. The type of the expression ~a does not match the representation type ~a." (display-type exptype) (display-type reptype)) (make-error-type)))))
Remember you will need to change both typeof (to do typechecking and evalaute the type of an up or down) and meval.
Answer: Extending our evaluator to support down is similar, except we have to check the value matches the abstract type.See clueval-mine.ss for the full code I used.(define (down? expr) (tagged-list? expr 'down)) (define (down-type expr) (cadr expr)) (define (down-expr expr) (caddr expr)) (define (meval expr env) (cond ... ((down? expr) (meval (down-expr expr) env)) ... ) ) (define (typeof-down expr env) (let ((exptype (typeof (down-expr expr) env)) (reptype (environment-lookup-value (down-type expr) env))) (if (type-match exptype (make-abstract-type (down-type expr))) reptype (begin (printf "Down type error. The type of the expression ~a does not match the abstract type ~a." (display-type exptype) (display-type (make-abstract-type (down-type expr)))) (make-error-type))))) (define (typeof expr env) (cond ... ((down? expr) (typeof-down expr env)) ... ))
