University of Virginia, Department of Computer Science
CS200: Computer Science, Spring 2004

Notes: Friday 23 January 2004
Schedule

GEB Reading Guide
As you read GEB Little Harmonic Labyrinth and Chapter 5, here are some things to think about:

Richard Feynman won the Nobel Prize in Physics in 1965 and was important in the Manhattan Project and in the Space Shuttle Challenger investigation. He also made important contributions to Computer Science (a few of which we will see later in this class). In 1984, Richard Feynman and Gerry Sussman co-taught a course at Caltech using an early version of the Wizard Book. Here's a story about that from Feynman Online ( For more stories about Feynman, "Surely You're Joking, Mr. Feynman!": Adventures of a Curious Character is highly recommended summer reading.):

In the beginning part of 1984, Feynman was teaching a course on computing at Caltech. The course was also co-jointly taught by Gerald Sussman from MIT. On one occasion Feynman was lecturing at the blackboard, but this time Sussman kept coming up and correcting him. Later that week Feynman was supposed to come over for dinner. On the night in question, Feynman's wife Gweneth called to say that Feynman was in the hospital and that they would not be able to come over. She told me not to tell anyone, as she didn't want the word to get around. Apparently Feynman in his excitement to purchase a new computer tripped on the sidewalk curb and hit his head. This caused some internal complications and bleeding. In a week or so, Feynman was back on his feet and returned to class. At lunch Feynman related what had happened. After bumping his head, he paid little or no attention to it. He was bleeding when he entered the computer store. What was interesting is that he gradually began to loose his sense of what was happening around him without internally realizing it. First, he couldn't locate his car. Then he had a very strange session with one of his artistic models. And on another day, he told his secretary Helen Tuck that he was going home, and proceeded to undress and lie down in his office. He forgot that he was to give a lecture at Hughes aircraft, and so on... Everything was just rationalized away. But you know, he said, NO ONE told me I was going crazy. Now why not? I said, Come on. You are always doing weird stuff. Besides there such a fine line between genius and madness that it sometimes difficult to tell! Listen, ape, the next time I go crazy around here, you be sure to tell me!
Evaluation Rules
(define square (lambda (x) (* x x)))
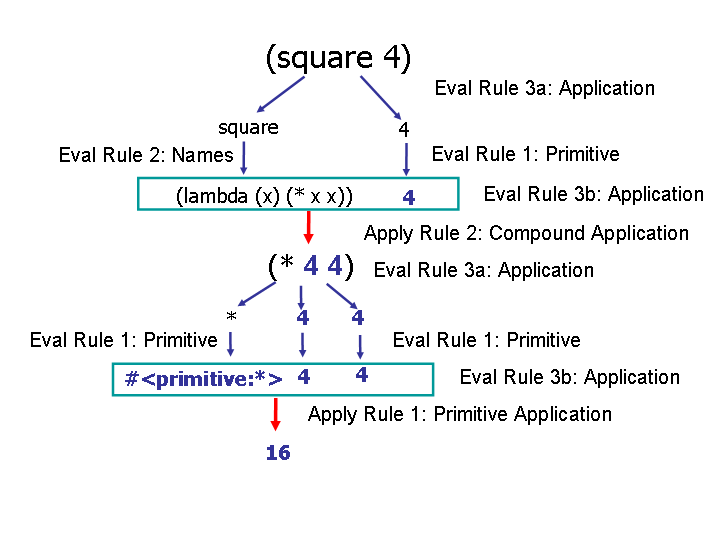
Expression ::= (define Name Expression)
Eval 4-define. If the expression is (define Name Expression) associate the Expression with Name (for Evaluation Rule 2).

So, the expression associated with square is (lambda (x) (* x x)).

(square 4)
Expression ::= (Expression ExpressionList)
Evaluation Rule 3: Application. If the expression is an application:
    (a) Evaluate all the subexpressions of the combination (in any order)
    (b) Apply the value of the first subexpression to the values of all the other subexpressions.

So, we need to evaluate the subexpressions according to rule 3a:

square is a name
Expression ::= Name
Evaluation Rule 2: Names. If the expression is a name, it evaluates to the value associated with that name.
The expression associated with square is (lambda (x) (* x x)).

Evaluate (lambda (x) (* x x))

Expression ::= (lambda (Parameters) Expression)
Eval 4-lambda. Lambda expressions self-evaluate. (Do not do anything until it is applied.)

So, square evaluates to (lambda (x) (* x x)).

4 is a primitive
Expression ::= Primitive
Evaluation Rule 1: Primitives. If the expression is a primitive, it is self-evaluating.

4 evaluates to the number 4. Apply the value of the first subexpression to the values of all the other subexpressions.

So, we are applying (lambda (x) (* x x)) to 4. Since (lambda (x) (* x x)) is a compound procedure, we use apply rule 2:
Application Rule 2: Compound Procedures. If the procedure is a compound procedure, evaluate the body of the procedure with each formal parameter replaced by the corresponding actual argument expression value.
The body of the procedure is (* x x). The name of the first parameter is x which corresponds to the first argument expression value, 4. So, we need to evaluate (* x x) with each x replaced by 4: (* 4 4).

Expression ::= (Expression ExpressionList)
Evaluation Rule 3: Application. If the expression is an application:
    (a) Evaluate all the subexpressions of the combination (in any order)
    (b) Apply the value of the first subexpression to the values of all the other subexpressions.

Rule 3a tells us to evaluate each sub-expression: * is a primitive that self-evaluates to the primitive procedure *, 4 is the value 4.

Rule 3b tells us to apply the value of the first subexpression, the primitive procedure * to the values of all the other subexpressions. since * is a primitive procedure, we use application rule 1:

Application Rule 1: Primitives. If the procedure to apply is a primitive, just do it.
Hence, (* 4 4) evaluates to 16 and the original expression (square 4) evaluates to 16 (as one would hope).
Defining Recursive Procedures
  1. Be optimistic.
    • Assume you can solve it.
    • If you could, how would you solve a bigger problem.
  2. Think of the simplest version of the problem, something you can already solve.
    • This is called the base case.
    • Usually something like solve for 0 or the empty list
  3. Combine them to solve the problem. 
(define (find-closest goal numbers)
  (if (= 1 (length numbers))
      (first numbers)
      (if (< (abs (- goal (first numbers)))
	     (abs (- goal 
		     (find-closest goal (rest numbers)))))
	  (first numbers)
	  (find-closest goal (rest numbers))))
Links
cs200-staff@cs.virginia.edu
Using these Materials