Day 2: Public-Key Cryptography

How well can this work in Alice and Bob have never met before?

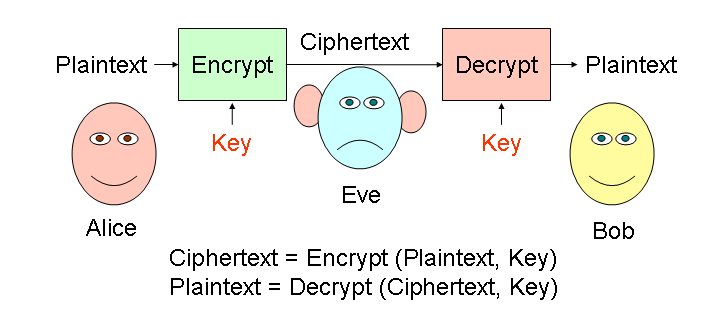
Public-Key Cryptography

We need to use different keys for encrypting and decrypting. That way, Alice can send Bob a message without needing to set up a secret key first. All she needs to know if Bob's public key. Anyone else can know Bob's public key, but that isn't enough to decrypt the message.

This means we need a problem that is:

1. Hard to do in one direction (decryption)
2. Easy to do in the other direction (encryption)

Finding prime factors!

1. Given a big number, it is hard to find its prime factors.
2. But, it is easy to multiple any two numbers together.

Modular Exponentiation

We can calculate any number mod n by just subtracting multiples of n until we get to a number less than n. So,

5 mod 7 = 5                  5 is already less than 7

8 mod 7 = 1                  since 8 - 7 = 1

17 mod 7 = 3                 since 17 - (2 * 7) = 3

Questions

1. 9 mod 7

2. 2 mod 3

3. 3 mod 2

4. 100 mod 11

5. 1024 mod 1022

Modular exponentiation is like modular arithmetic, except the numbers are much bigger. But, because it is modulo it is actually easier to calculate.

53 = 5 * 5 * 5 = 125
125 mod 7 = 6

But, it is easier to calculate:

53 mod 7 = 5 * 5 * 5 mod 7
                    = (5 * 5 mod 7) * 5 mod 7
                    = (25 mod 7) * 5 mod 7
                    =     4      * 5 mod 7
                    =     20 mod 7
                    =      6

Questions

6. 3² mod 7

7. 3³ mod 7

8. 3³ mod 15

9. 3⁷ mod 15

RSA Algorithm

Setup

1. Bob chooses two secret prime numbers. We will call them p and q. To be secure, the numbers must be very big (at least 100 digits).
2. Bob calculates n = p * q.
3. Bob finds a number e where the greatest common divisor of e and (p - 1) * (q - 1) is 1.
4. Bob finds a number d where d * e = 1 mod ((p - 1) * (q - 1)).
5. Bob publishes n and e as the public key. He keeps d secret and destroys p and q.

Encryption

Ciphertext = M^e mod n

Decryption

Message = C^d mod n

Questions

1. Select two secret prime numbers: p = 3, q = 5.

2. Calculate n = p * q = __________________

3. Select e such that the greatest common divisor of e and (p - 1) * (q - 1) is 1:

   GCD (e, 8) = 1

   Which one of these would be a possible choice for e:
   1. 2
   2. 4
   3. 6
   4. 7

4. Select d such that d * e = 1 mod ((p - 1) * (q - 1)). Which one of these would be a possible choice for d:
   1. 4
   2. 6
   3. 7
   4. 8
   Encryption Encrypt the message M = 3.

   C = M ^e mod n

   
   

   
   

   
   

   
   

   
   

   
   Decryption Decrypt the ciphertext C = 12.

   M = C ^d mod n