Homework J5

Due: Friday, Oct 28 2005 by 10 a.m.

Purpose

In this assignment you will get additional experience programming with loop constructs and manipulating mathematical code, while exercising your problem-solving skills to construct a solution to a less-explicitly specified problem than in previous homeworks. You will also be exposed to Java's BigDecimal class for performing arbitrary-precision floating point arithmetic -- a BigInteger can represent an integer of any size; a BigDecimal can represent a floating-point number with any number of digits after the decimal point. Your code should be in a class named PrimeSearch (and thus a file named PrimeSearch.java).

Background

A couple of years ago, Google ran a recruiting campaign in which the following billboard appeared with no further explanation:

The text of the billboard reads:

{first 10-digit prime found in consecutive digits of e}.com

In other words, the billboard directed viewers to a web site whose address was <some ten-digit number>.com. The idea is that if you were smart enough to figure out the proper ten-digit number, which as the billboard says is the first ten-digit prime to appear in consecutive digits of the irrational constant e, you were a prospective Google employee. The website then had other puzzles and programming challenges, and if you passed those it would eventually accept your resume for a fast-track interview.

Your assignment is to calculate e to sufficient precision that you can recover the first 10-digit prime found in its digits.

Computing e

The number e is the base of natural logarithms and one of the most important numbers. You can learn why and read a great deal about it here. The first few digits of e are 2.71828183, but the constant is irrational, meaning that its digits never fall into a repeating pattern. The constant has been computed to an absurd number of digits over the years, but although you can find lists of the first few million digits of e on the web, for this assignment you must compute it directly. There are many algorithms for generating the digits of e, but for this assignment you should use the following simple formulation for computing e:

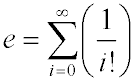
or, in other words

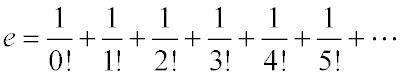
If you evaluate enough terms in this series, you will determine e to sufficient precision to solve the Google puzzle. For the purposes of this assignment, we will tell you in advance that 500 terms will provide sufficient precision to solve the puzzle.

Remember that the ! symbol here indicates factorial. For example, 4! = 4 * 3 * 2 * 1, and 5! = 5 * 4 * 3* 2 * 1, and so on. For your first programming task, you will need to write Java code using loops to calculate the factorial of a number. The factorial function grows large rapidly; the denominator in this series gets very big very quickly, so you'll need to represent it using a BigInteger object.

Of course, this means the fractions themselves get small rather quickly, so you'll use the Java BigDecimal class to represent each term and the running total. As you will see from the Java documentation, the BigDecimal class uses the MathContext class to specify the amount of precision necessary - essentially, the MathContext.scale field is the number of digits to keep after the decimal point. For the purposes of this assignment, we will tell you in advance that 500 digits will provide sufficient precision to solve the puzzle. Of course, this implies that the 10-digit prime that you are looking for is to be found in the first 500 consecutive digits of e, but we are telling you in advance that this is the case.

Once you've calculated e to sufficient precision, we suggest you convert it to a String and use the substring method to extract candidate 10-digit numbers, convert them back to BigInteger and use the BigInteger.isProbablePrime() method to test primality. If this method indicates that the number is probably prime, you need to verify absolutely that this is the case. You can use code from the previous assignment (you are welcome to reuse your own code, though be sure to use BigInteger) to verify absolutely that the number is prime. Your code may take a LONG time to determine this, so be warned!

Suggested approach

We suggest that you break the assignment down into the following pieces. You should implement, test, and debug each piece independently until you are confident that it works correctly, and only then hook the pieces together to solve the final puzzle. All parts can be done within the main() method.

Compute factorial: the first code segment should compute the factorial of an integer. Start by computing factorials using int variables, then extend your code to use BigInteger instead when you are confident it is working, then test your code again to verify the correctness of your BigInteger implementation.
Compute e: the second part computes e using the sum of n terms in the series given above, where n is input by the user. Start by using double variables to represent the sum and the fractional terms, then convert the code to use BigDecimal types instead and test it again. Finally, you may wish to test against a known value of e as described below.
Find probable primes: the third part will search the digits of e, either read from a file or computed as described above, and use BigInteger's isProbablePrime() method to check for primality. The isProbablePrime() method will need a confidence to which primality is tested as it's parameter; a value of about 10 will provide sufficient precision. Check the answers you get against the 8- and 9-digit primes given below.
Exhaustive primality testing: implement a loop to exhaustively test the possible factors of the probable prime you have identified. This can take a very long time (minutes) for a 10-digit prime. To speed it up you may want to optimize your code to run faster, for example by testing 2 first, and (assuming that 2 is not a factor) using a loop which skips all even numbers (since they cannot be factors if 2 was not a factor). This will make your code run about twice as fast, since it is only checking half as many numbers. You can also check factors only up to the square root of the number being tested (convert it to double and use the Math.sqrt() method). Which of these two optimizations will make a bigger difference for a 10-digit prime? Write your answer as a comment in your file.

Test code

For testing purposes you should explicitly test your factorial code, explicitly test your code for computing e, and try finding the first 8-digit prime in consecutive digits of e (72407663, found spanning digits 65 to 72) and first 9-digit prime (360287471, spanning digits 20 to 28). For testing your code to compute e, you may wish to use a known list of digits such as this. Of course, you are not allowed to use such a list in the final computation (except for partial credit if you run out of time). Describe the testing you performed in the comments and include the code you used for the test.

More about `MathContext`

The use of the MathContext object is a little confusing. Here are a couple of lines of code that give an example of how to declare a MathContext object of the required precision, use it to declare a BigDecimal of that precision, and perform an arithmetic operation at that precision:

    // Declare a MathContext object representing sufficient precision:
    final int NUM_DIGITS = 500;
    MathContext hiPrecision = new MathContext(NUM_DIGITS);
    
    // Declare two BigDecimal object variables at that precision:
    BigDecimal result = new BigDecimal(0, hiPrecision); 
    BigDecimal one = new BigDecimal(1, hiPrecision);
    
    // Add them together at the required precision and store in "result":
    result = result.add(one, hiPrecision);

Helpful Hints

To convert from a BigInteger (named bigI, for example) to a BigDecimal, you can use the following code, where hiPrecision is the MathContext from above.

BigDecimal bigD = new BigDecimal(bigI, hiPrecision);

To convert from a int to a BigInteger, you first have to convert it to a String. Then, you can convert the String to a BigInteger. You can use the following code to do it in one go (x is your int variable).

BigInteger bigI = new BigInteger (String.valueOf(x));

Submission

When you are finished, submit your PrimeSearch.java file.