 |
|
Homework J5Due: Friday, Oct 28 2005 by 10 a.m. |
In this assignment you will get additional experience programming with loop constructs and manipulating mathematical code, while exercising your problem-solving skills to construct a solution to a less-explicitly specified problem than in previous homeworks. You will also be exposed to Java's BigDecimal class for performing arbitrary-precision floating point arithmetic -- a BigInteger can represent an integer of any size; a BigDecimal can represent a floating-point number with any number of digits after the decimal point. Your code should be in a class named PrimeSearch (and thus a file named PrimeSearch.java).
A couple of years ago, Google ran a recruiting campaign in which the following billboard appeared with no further explanation:

The text of the billboard reads:
{first 10-digit prime found in consecutive digits of e}.com
In other words, the billboard directed viewers to a web site whose address was <some ten-digit number>.com. The idea is that if you were smart enough to figure out the proper ten-digit number, which as the billboard says is the first ten-digit prime to appear in consecutive digits of the irrational constant e, you were a prospective Google employee. The website then had other puzzles and programming challenges, and if you passed those it would eventually accept your resume for a fast-track interview.
Your assignment is to calculate e to sufficient precision that you can recover the first 10-digit prime found in its digits.
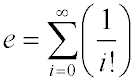
or, in other words
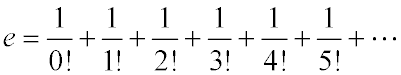
If you evaluate enough terms in this series, you will determine e to sufficient precision to solve the Google puzzle. For the purposes of this assignment, we will tell you in advance that 500 terms will provide sufficient precision to solve the puzzle.
Remember that the ! symbol here indicates factorial. For example, 4! = 4 * 3 * 2 * 1, and 5! = 5 * 4 * 3* 2 * 1, and so on. For your first programming task, you will need to write Java code using loops to calculate the factorial of a number. The factorial function grows large rapidly; the denominator in this series gets very big very quickly, so you'll need to represent it using a BigInteger object.
Of course, this means the fractions themselves get small rather quickly, so you'll use the Java BigDecimal class to represent each term and the running total. As you will see from the Java documentation, the BigDecimal class uses the MathContext class to specify the amount of precision necessary - essentially, the MathContext.scale field is the number of digits to keep after the decimal point. For the purposes of this assignment, we will tell you in advance that 500 digits will provide sufficient precision to solve the puzzle. Of course, this implies that the 10-digit prime that you are looking for is to be found in the first 500 consecutive digits of e, but we are telling you in advance that this is the case.
Once you've calculated e to sufficient precision, we suggest you convert it to a String and use the substring method to extract candidate 10-digit numbers, convert them back to BigInteger and use the BigInteger.isProbablePrime() method to test primality. If this method indicates that the number is probably prime, you need to verify absolutely that this is the case. You can use code from the previous assignment (you are welcome to reuse your own code, though be sure to use BigInteger) to verify absolutely that the number is prime. Your code may take a LONG time to determine this, so be warned!
We suggest that you break the assignment down into the following pieces. You should implement, test, and debug each piece independently until you are confident that it works correctly, and only then hook the pieces together to solve the final puzzle. All parts can be done within the main() method.
The use of the MathContext object is a little confusing. Here are a couple of lines of code that give an example of how to declare a MathContext object of the required precision, use it to declare a BigDecimal of that precision, and perform an arithmetic operation at that precision:
// Declare a MathContext object representing sufficient precision:
final int NUM_DIGITS = 500;
MathContext hiPrecision = new MathContext(NUM_DIGITS);
// Declare two BigDecimal object variables at that precision:
BigDecimal result = new BigDecimal(0, hiPrecision);
BigDecimal one = new BigDecimal(1, hiPrecision);
// Add them together at the required precision and store in "result":
result = result.add(one, hiPrecision);
To convert from a BigInteger (named bigI, for example) to a BigDecimal, you can use the following code, where hiPrecision is the MathContext from above.
BigDecimal bigD = new BigDecimal(bigI, hiPrecision);
To convert from a int to a BigInteger, you first have to convert it to a String. Then, you can convert the String to a BigInteger. You can use the following code to do it in one go (x is your int variable).
BigInteger bigI = new BigInteger (String.valueOf(x));
When you are finished, submit your PrimeSearch.java file.